一次课外实践活动中，一个小组测量旗杆的高度如图，在A处用测角仪（离地高度为1.2米）测得旗杆顶端的仰角为15°，朝旗杆方向前进20米到B处，再次测得旗杆顶端的仰角为30°，求旗杆EG的高度．

解：由已知∠ECD=15°，∠EDF=30°，
所以∠CED=15°，
∴∠CED=∠ECD，
∴DC=DE=20，
在Rt△DEF中，
由 $\text{[math]}$ ，得：
EF=DE•sin∠EDF=20×sin30°=10，
又FG=CA=1.2米，
因此EG=EF+FG=10+1.2=11.2（米），
答：旗杆EG的高度为11.2米．
分析：首先分析图形：根据题意构造直角三角形，利用在Rt△DEF中，由 $\text{[math]}$ ，得出EF的长度，进而可求出答案．
点评：此题主要考查了仰角问题应用，要求学生借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

在一次课外实践活动中，有两个课题学习小组分别用测倾器、皮尺测量旗杆和小山的高度，他们分别设计了如下方案：
第一组，测量旗杆（图-）：①在测点A处安置测倾器，测得旗杆顶部M的仰角∠MCE=α；②量出测点A到旗杆底部N的水平距离AN=m；量出测倾器的高度AC=h．
第二组，测量某小山的高度（图二），他们测量时所填写的表格如下：

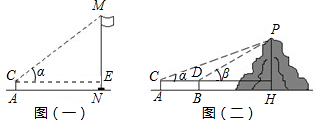
题目	测量小山的高度
测量数据	测量项目		测倾器高度
	仰角α	20°30′	1.2米
	仰角β	30°	小山高度
	AB的距离

（1）请你求出旗杆的高度（用已知的字母表示）；
（2）第二小组记录的同学不小心将AB的距离弄模糊了，请你填上一个较合理的数据，并由此求出小山PH的高度（结果精确到个位）．

查看答案和解析>>

科目：初中数学 来源： 题型：

在一次课外实践活动中，同学们要测湘江河的宽度．如图1所示，小明先在河西选定建筑物A，并在河东岸的B处观察，此时视线BA在河岸BE所成的夹角∠ABE=32°，小明沿河岸BE走了400

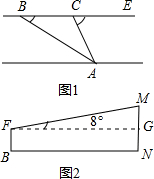米到C处，再观察A，此时视线CA与河岸所成的夹角∠ACE=64°．
（1）请你根据以上数据，帮助小明计算出湘江河的宽度（结果精确到0.1米）．
（2）求出湘江河宽后，小明突发奇想，欲求B的正对岸建筑物的高度MN（如图2所示），现测得小明的眼睛与地面的距离（FB）是1.6m，看建筑物顶部M的仰角（∠MFG）是8°，BN为湘江河宽，求建筑物的高度MN（结果精确到0.1米）．
（提示：河的两岸互相平行；参考数值：sin32°≈0.530；cos32°≈0.848；
tan32°≈0.625；sin64°≈0.900；cos64°≈0.438；tan64°≈2.050；
sin8°≈0.139；cos8°≈0.990；tan8°≈0.141）

查看答案和解析>>

科目：初中数学 来源： 题型：

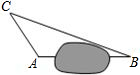在一次课外实践活动中，同学们要知道校园内A，B两处的距离，但无法直接测得．已知校园内A、B、C三点形成的三角形如图所示，现测得AC=6m，BC=14m，∠CAB=120°，请计算A，B两处之间的距离．

查看答案和解析>>

科目：初中数学 来源： 题型：

（2010•市南区模拟）在一次课外实践活动中，同学们要测量某公园人工湖两侧A、B两个凉亭之间的距离．现测得AC=30m，∠B=37°，∠CAE=64°，请你求出A、B两个凉亭之间的距离（结果精确到1m）．（参考数据：sin37°≈

，tan37°≈

，sin64°≈

，cos64°≈

）

查看答案和解析>>

科目：初中数学 来源： 题型：

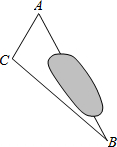在一次课外实践活动中，同学们要知道校园内A、B两处的距离，但无法直接测得．已知校园内A、B、C三点形成的三角形如图所示，现测得AC=6m，BC=14m，∠CAB=60°，请计算A、B两处之间的距离．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学

一次课外实践活动中，一个小组测量旗杆的高度如图，在A处用测角仪（离地高度为1.2米）测得旗杆顶端的仰角为15°，朝旗杆方向前进20米到B处，再次测得旗杆顶端的仰角为30°，求旗杆EG的高度．