
下列等式从左到右的变形,属于因式分解的是
A. (a+b)(a﹣b)=a2﹣b2 B. a2+4a+1=a(a+4)+1
C. x3﹣x=x(x+1)(x﹣1) D. 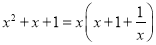
 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源:2016-2017学年陕西省七年级(下)第二次测验数学试卷 题型:填空题
﹣|﹣5|的相反数为_____.
5 【解析】根据绝对值的性质,化简为-|-5|=-5,再根据相反数的意义,可知-5的相反数为5. 故答案为:5.查看答案和解析>>
科目:初中数学 来源:安徽省16-17学年度第一学期七年级数学期末考试卷 题型:单选题
如图是一个正方体纸盒的展开图,每个面内都标注了字母或数字,则面a在展开前所对的面的数字是()
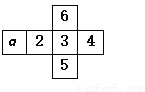
A. 2 B. 3 C. 4 D. 5
B 【解析】分析:由平面图形的折叠及立体图形的表面展开图的特点解题. 解答:【解析】 正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,所以面a在展开前所对的面的数字是3. 故选B.查看答案和解析>>
科目:初中数学 来源:山西农业大学附属中学2017-2018学年八年级上学期第三次月考数学试卷 题型:解答题
化简下列多项式:
(1)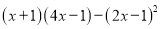
(2)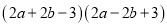
(3)若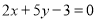 ,求
,求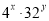 的值.
的值.
(4)先化简,再求值:(2x﹣1)2﹣(3x+1)(3x﹣1)+5x(x﹣1),其中x=﹣2.
(1) (2) (3)8;(4)20. 【解析】(1)先利用多项式的乘法计算,再运用完全平方公式计算即可;(2)利用平方差公式计算即可;(3)利用幂的乘方,同底数幂的乘法的逆运算计算即可;(4)原式利用平方差公式,完全平方公式,以及单项式乘以多项式法则计算得到最简结果,把x的值代入计算即可求出值. 本题解析: (1)= , (2)原式= , (3)∵2x+5y=3, ...查看答案和解析>>
科目:初中数学 来源:山西农业大学附属中学2017-2018学年八年级上学期第三次月考数学试卷 题型:单选题
如图,Rt△ABC中,∠C=90°,∠B=45°,AD是∠CAB的平分线,DE⊥AB于E,AB=a,CD=m,则AC的长为
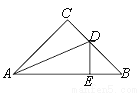
A. 2m B. a﹣m C. a D. a+m
B 【解析】:∵AD是∠CAB的平分线,DE⊥AB,∠C=90°, ∴CD=DE, 在Rt△ACD和Rt△AED中, , ∴Rt△ACD≌Rt△AED(HL), ∴AC=AE, ∵∠B=45°,DE⊥AB, ∴△BDE是等腰直角三角形, ∴BE=DE=m, ∵AE=AB-BE=a-m, ∴AC=a-m. 故选B.查看答案和解析>>
科目:初中数学 来源:黑龙江省哈尔滨市香坊区2017年中考数学二模试卷(解析版) 题型:解答题
某文教店老板到批发市场选购A,B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍.
(1)求A,B两种品牌套装每套进价分别为多少元?
(2)若A品牌套装每套售价为13元,B品牌套装每套售价为9.5元,店老板决定,购进B品牌的数量比购进A品牌的数量的2倍还多4套,两种工具套装全部售出后,要使总的获利超过120元,则最少购进A品牌工具套装多少套?
【答案】(1)A种品牌套装每套进价为10元,B种品牌套装每套进价为7.5元;(2)最少购进A品牌工具套装17套.
【解析】试题分析:(1)利用两种套装的套数作为等量关系列方程求解.(2)利用总获利大于等于120,解不等式.
试题解析:
(1)【解析】
设B种品牌套装每套进价为x元,则A种品牌套装每套进价为(x+2.5)元.
根据题意得: 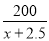 =2×
=2×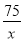 ,
,
解得:x=7.5,
经检验,x=7.5为分式方程的解,
∴x+2.5=10.
答:A种品牌套装每套进价为10元,B种品牌套装每套进价为7.5元.
(2)【解析】
设购进A品牌工具套装a套,则购进B品牌工具套装(2a+4)套,
根据题意得:(13﹣10)a+(9.5﹣7.5)(2a+4)>120,
解得:a>16,
∵a为正整数,
∴a取最小值17.
答:最少购进A品牌工具套装17套.
点睛:分式方程应用题:一设,一般题里有两个有关联的未知量,先设出一个未知量,并找出两个未知量的联系;二列,找等量关系,列方程,这个时候应该注意的是和差分倍关系:三解,正确解分式方程;四验,应用题要双检验;五答,应用题要写答.
【题型】解答题
【结束】
26
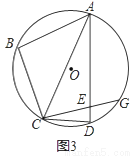
四边形ABCD内接于⊙O,点E为AD上一点,连接AC,CB,∠B=∠AEC.
(1)如图1,求证:CE=CD;
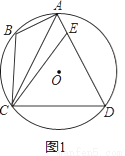
(2)如图2,若∠B+∠CAE=120°,∠ACD=2∠BAC,求∠BAD的度数;
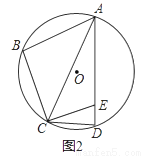
(3)如图3,在(2)的条件下,延长CE交⊙O于点G,若tan∠BAC= 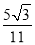 ,EG=2,求AE的长.
,EG=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源:黑龙江省哈尔滨市香坊区2017年中考数学二模试卷(解析版) 题型:填空题
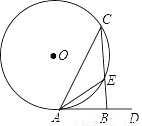
如图,在⊙O中,AC是弦,AD是切线,CB⊥AD于B,CB与⊙O相交于点E,连接AE,若AE平分∠BAC,BE=1,则CE=________.
【答案】2
【解析】∵AD是切线,  ∠EAB=∠C,
∠EAB=∠C,
∵AE是角平分线,
∠CAE=∠EAB,
 ∠CAE=∠EAB=∠C,
∠CAE=∠EAB=∠C,
∵CB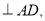
 ∠C+∠CAB=90°,
∠C+∠CAB=90°,
 3∠C=90°,
3∠C=90°,
 ∠C=30°.
∠C=30°.
故答案为30°.
【题型】填空题
【结束】
19
在?ABCD中(非矩形),连接AC,△ABC为直角三角形,若AB=4,AC=3,则AD=________.
或5 【解析】(1)如图,四边形是平行四边形,利用勾股定理知,CD=AB,AD= (2) 四边形是平行四边形,利用勾股定理知,BC=AD=.查看答案和解析>>
科目:初中数学 来源:黑龙江省哈尔滨市香坊区2017年中考数学二模试卷(解析版) 题型:单选题
下列各式中,运算结果正确的是( )
A. (﹣1)3+(﹣3.14)0+2﹣1=﹣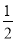 B. 2x﹣2=
B. 2x﹣2= 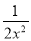
C. 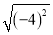 =﹣4 D. a2•a3=a5
=﹣4 D. a2•a3=a5
查看答案和解析>>
科目:初中数学 来源:广州市2018学年度七年级(上)数学期末测试卷 题型:单选题
如图,OC是平角∠AOB的平分线,OD、OE分别是∠AOC和∠BOC的平分线,图中和∠COD互补的角有( )个
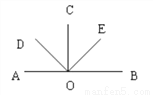
A. 1 B. 2 C. 3 D. 0
B 【解析】试题解析:∵OC是平角∠AOB的平分线, ∵OD、OE分别是∠AOC和∠BOC的平分线, ∴ 都与∠DOC互补, ∴图中和∠COD互补的角有2个. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com