
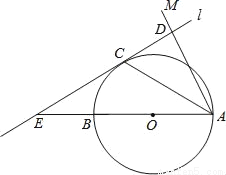
如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若直线l与AB的延长线相交于点E,⊙O的半径为3,并且∠CAB=30°,求CE的长.
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:解答题
计算:(﹣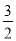 )2÷(﹣
)2÷(﹣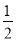 )2×(1
)2×(1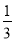 )2﹣(﹣4)2﹣42.
)2﹣(﹣4)2﹣42.
查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:单选题
下列变形正确的是( )
A. 4x﹣5=3x+2变形得4x﹣3x=﹣2+5
B. 3x=2变形得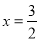
C. 3(x﹣1)=2(x+3)变形得3x﹣1=2x+6
D. 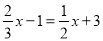 变形得4x﹣6=3x+18
变形得4x﹣6=3x+18
查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:单选题
如图,直线l和双曲线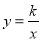 (k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
(k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
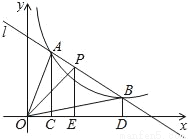
A. S1<S2<S3 B. S1>S2>S3 C. S1=S2>S3 D. S1=S2<S3
D 【解析】根据反比例函数k的几何意义可得S1= S2<S3,故选D.查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:单选题
下列方程的变形正确的是( )
A. 由2x﹣3=4x,得:2x=4x﹣3
B. 由7x﹣4=3﹣2x,得:7x+2x=3﹣4
C. 由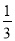 x﹣
x﹣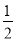 =3x+4得﹣
=3x+4得﹣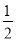 ﹣4=3x+
﹣4=3x+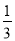 x
x
D. 由3x﹣4=7x+5得:3x﹣7x=5+4
D 【解析】试题分析:A、由2x-3=4x,得:2x=4x+3,不符合题意; B、由7x-4=3-2x,得:7x+2x=3+4,不符合题意; C、由x﹣=3x+4,得:﹣﹣4=3x+x,不符合题意; D、由3x-4=7x+5得:3x-7x=5+4,符合题意, 故选D.查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(八) 题型:填空题
观察下列等式:
1×2=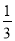 ×(1×2×3﹣0×1×2)
×(1×2×3﹣0×1×2)
2×3=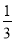 ×(2×3×4﹣1×2×3)
×(2×3×4﹣1×2×3)
3×4=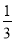 ×(3×4×5﹣2×3×4)
×(3×4×5﹣2×3×4)
…
计算:3×[1×2+2×3+3×4+…+n(n+1)]=_____.
n(n+1)(n+2) 【解析】试题解析:∵1×2=×(1×2×3-0×1×2) 2×3=×(2×3×4-1×2×3), 3×4=×(3×4×5-2×3×4), …, ∴n(n+1)= [n(n+1)(n+2)-(n-1)n(n+1)], ∴3×[1×2+2×3+3×4+…+n(n+1)] =3× [1×2×3-0×1×2+2×3×4-1×2×3+3×4×...查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(八) 题型:填空题
若代数式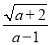 有意义,则a的取值范围为_____.
有意义,则a的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源:2017年山东省临沂市中考数学二模试卷(一) 题型:解答题
计算:(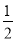 )﹣2﹣(π﹣3.14)0+
)﹣2﹣(π﹣3.14)0+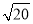 ﹣|2﹣
﹣|2﹣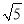 |.
|.
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
如图,点D、E是等边△ABC的边BC、AC上的点,且CD=AE,AD、BE相交于P点,BQ⊥AD于Q,已知PE=1,PQ=3,则AD等于( )
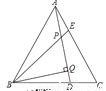
A. 5 B. 6 C. 7 D. 8
C 【解析】试题分析:∵△ABC是等边三角形,∴AB=AC,∠BAC=∠C=60°,又AE=CD, ∴△ABE≌△CAD(SAS), ∴∠ABE=∠CAD, ∴∠BPD=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°,∵BQ⊥AD,∴∠PBQ=30°, ∴BP=2PQ=2×3=6,∴AD=BE=BP+PE=6+1=7.故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com