
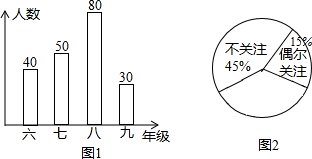
分析 (1)根据扇形统计图找出关注“送戏下乡”活动的百分比,乘以1600即可得到结果;
(2)画树状图得出所有等可能的情况数,找出恰好是甲与乙的情况,即可确定出所求概率.
解答 解:(1)1600×(1-45%)=880(人).
∴该校关注本次“送戏下乡”的学生大约有880人.
(2)画树状图,如图所示:
由图可知,共有12种等可能结果,其中恰好是甲和乙的有2种结果.
∴P(恰好是甲和乙)=$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查的是条形统计图和扇形统计图以及求随机事件的概率问题的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A、B两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,其中k>0,AC⊥y轴于点C,BD⊥x轴于点D,且AC=1
如图,A、B两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,其中k>0,AC⊥y轴于点C,BD⊥x轴于点D,且AC=1查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB与y轴交于点C.
已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
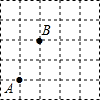 在如图的方格纸中,每个小方格都是边长为1的正方形,点A、B是方格中的两个格点(即网格中横、纵线的交点),在这个5×5的方格纸中,格点C使△ABC的面积为2个平方单位,则图中这样的点C有( )个.
在如图的方格纸中,每个小方格都是边长为1的正方形,点A、B是方格中的两个格点(即网格中横、纵线的交点),在这个5×5的方格纸中,格点C使△ABC的面积为2个平方单位,则图中这样的点C有( )个.| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com