
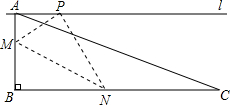
 如图,在三角形纸片ABC中,∠ABC=90°,AB=5,BC=13,过点A,作直线l∥BC,折叠三角形纸片ABC,使点B落在直线l上的P处,折痕为MN.当点P在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,若设AP的长为x,MN的长为y,则下列选项,能表示y与x之间的函数关系的大致图象是( )
如图,在三角形纸片ABC中,∠ABC=90°,AB=5,BC=13,过点A,作直线l∥BC,折叠三角形纸片ABC,使点B落在直线l上的P处,折痕为MN.当点P在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,若设AP的长为x,MN的长为y,则下列选项,能表示y与x之间的函数关系的大致图象是( )| A. |  | B. | 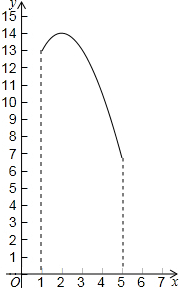 | ||
| C. | 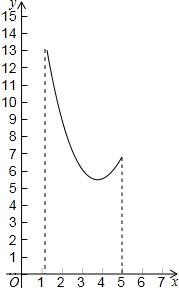 | D. | 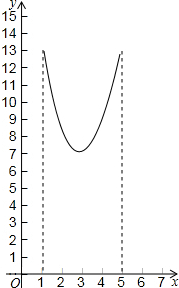 |
分析 首先确定自变量x的取值范围,利用勾股定理、相似三角形,构建函数关系式即可判断.
解答 解:如图1中,作CG⊥AP于G.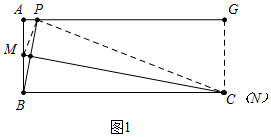
当点N与C重合时,在Rt△PGC中,∵∠G=90°,PC=CB=13,CG=AB=5,
∴PG=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∴PA=1,
如图2中,当M与A重合时,易知AP=5,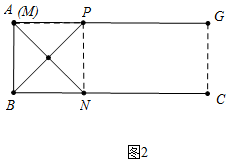
∵定端点M、N分别在AB、BC边上移动,
∴1≤x≤5,观察图A、B、C、D都是正确的.
如图3中,设MP=MB=a,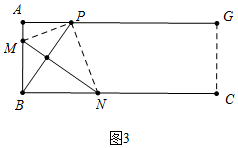
在Rt△AMP中,a2=x2+(5-a)2,
∴a=$\frac{{x}^{2}+25}{10}$,
由△APB∽△BMN,可得$\frac{AP}{BM}$=$\frac{PB}{MN}$,
∴$\frac{x}{\frac{{x}^{2}+25}{10}}$=$\frac{\sqrt{{x}^{2}+25}}{y}$,
∴y=$\frac{({x}^{2}+25)•\sqrt{{x}^{2}+25}}{10x}$,
观察图象可知:A、B、D是错误的(取特殊点代入判断即可).
故选C.
点评 本题考查动点问题函数图象、勾股定理、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,学会取特殊点解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
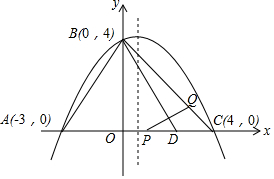 如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.
如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,E、F分别为正方形ABCD的边AB、AD上的点,且AE=AF,连接EF,将△AEF绕点A逆时针旋转45°,使E落在E1,F落在F1,连接BE1并延长交DF1于点G,如果AB=2$\sqrt{2}$,AE=1,则DG=$\frac{4\sqrt{5}}{5}$.
如图,E、F分别为正方形ABCD的边AB、AD上的点,且AE=AF,连接EF,将△AEF绕点A逆时针旋转45°,使E落在E1,F落在F1,连接BE1并延长交DF1于点G,如果AB=2$\sqrt{2}$,AE=1,则DG=$\frac{4\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
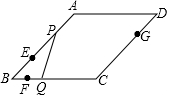 如图,在菱形ABCD中,∠ABC=45°,AB=6,点E、F、G分别是AB、BC、DC上的点,其中BE=DG=2,BF=1.点P从E点出发,以每秒2个单位长度沿折线EA-AD-DG运动;点Q以每秒1个单位沿折线FC-CG运动,当其中一个点到达后,另一个点也停止运动,设△BPQ的面积为S,点P,Q的运动时间为t秒,则S与t的函数关系的大致图象是( )
如图,在菱形ABCD中,∠ABC=45°,AB=6,点E、F、G分别是AB、BC、DC上的点,其中BE=DG=2,BF=1.点P从E点出发,以每秒2个单位长度沿折线EA-AD-DG运动;点Q以每秒1个单位沿折线FC-CG运动,当其中一个点到达后,另一个点也停止运动,设△BPQ的面积为S,点P,Q的运动时间为t秒,则S与t的函数关系的大致图象是( )| A. | 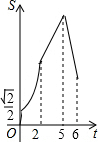 | B. | 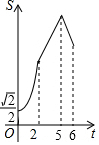 | C. | 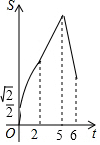 | D. | 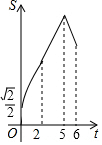 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 10 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com