
 AB=5,CF=
AB=5,CF= CD=12,由于AB∥CD,易得E、O、F三点共线,在Rt△AOE和Rt△OCF中,利用勾股定理分别计算出OE与OF,然后讨论:当圆心O在弦AB与CD之间时,AB与CD的距离=OE+OF;当圆心O在弦A′B′与CD的外部时,AB与CD的距离=OE-OF.
CD=12,由于AB∥CD,易得E、O、F三点共线,在Rt△AOE和Rt△OCF中,利用勾股定理分别计算出OE与OF,然后讨论:当圆心O在弦AB与CD之间时,AB与CD的距离=OE+OF;当圆心O在弦A′B′与CD的外部时,AB与CD的距离=OE-OF.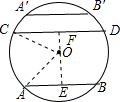
 AB=5,CF=
AB=5,CF= CD=12,
CD=12, =
= =5,
=5, =
=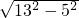 =12,
=12,

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com