
求抛物线y=x2-4x+3关于y轴对称的抛物线的表达式.
(1)在同一直角坐标系中,画出两抛物线;
(2)根据所画图像,说明两抛物线的关系.
|
[答案]∵- ∴抛物线y=x2-4x+3的顶点坐标为(2,-1). 由已知得,所求抛物线的开口方向和形状与原抛物线相同,其顶点与原抛物线的顶点关于 y轴对称.故所求抛物线的表达式为 y=(x+2)2-1,即y=x2+4x+3.(1)它们的图像如图所示.
(2)两抛物线开口方向相同,形状相同,只是位置不同,它们属于平移关系.即抛物线y=x2+4x+3也可看成抛物线y=x2-4x+3向左平移4个单位所得. [剖析]在对抛物线进行对称、平移等变换时,抛物线的形状不变,其顶点也被进行了相应变换.因此,在求变换后的表达式时,关键是确定其开口方向和顶点坐标. |
|
[方法提炼] 求抛物线关于 x轴、y轴、原点的对称图形的表达式时,先求出原抛物线的顶点坐标及对称抛物线的开口方向,再确定对称抛物线的顶点坐标,并写出其表达式. |


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源:学习周报 数学 沪科九年级版 2009-2010学年 第2期 总第158期 沪科版 题型:044
已知关于
x的一元二次方程x2+mx+n=0的两根是x1=-3,x2=4,求抛物线y=x2+mx+n的顶点坐标和对称轴.查看答案和解析>>
科目:初中数学 来源:新课程 新理念 新思维·同步练习篇·数学 九年级下册(苏教版) 苏教版 题型:044
先阅读下面一段材料,再完成后面的问题:
材料 过抛物线y=ax2(a>0)的对称轴上一点(0,-![]() ),作对称轴的垂线l,则抛物线上任意一点P到点F(0,
),作对称轴的垂线l,则抛物线上任意一点P到点F(0,![]() )的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0,
)的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0,![]() ).
).
问题 若直线y=kx+b交抛物线y=![]() x2于A、B两点,AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图).
x2于A、B两点,AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图).
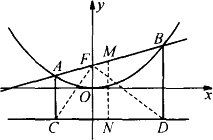
(1)求抛物线y=![]() x2的焦点F的坐标;
x2的焦点F的坐标;
(2)求证:直线AB过焦点时,CF⊥DF;
(3)当直线AB过点(-1,0),且以线段AB为直径的圆与准线l相切时,求这条直线对应的函数解析式.
查看答案和解析>>
科目:初中数学 来源:2011届河南省扶沟县初三下册26章《用函数观点看一元二次方程》检测题 题型:解答题
抛物线y=x2+x-k与直线y=-2x+1的交点的纵坐标为3。
(1)求抛物线的解析式
(2)求抛物线y=x2+x-k与直线y=-2x+1的另一个交点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com