练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示,AB-AC=2cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14cm,

    求AB和AC的长.

    AB=8,AC=6 【解析】试题分析：根据线段垂直平分线性质求出BD=DC，根据三角形周长求出AB+AC=12cm，根据已知得出AC=AB-2cm，即可求出答案． 试题解析： ∵DE垂直平分BC, ∴BD=CD. ∴△ACD的周长=AD+AC+CD=AD+AC+BD=AB+AC=14cm. 解方程组 得 ∴AC=6cm，AB=8cm.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版数学七年级下册第四章4.2图形的全等课时练习 题型：解答题

    已知△ABC≌△A′B′C′，∠C=25°，BC=6 cm，AC=4 cm，你能得出△A′B′C′中哪些角的大小，哪些边的长度？

    ∠C’=25°，B’C’=6 cm，A’C’=4cm 【解析】试题分析：根据全等三角形的性质即可得. 试题解析：∵△ABC≌△A′B′C′， ∴∠C′=∠C=25°， B′C′=BC=6cm， A′C′=AC=4cm.

    查看答案和解析>>

    科目：初中数学 来源：2017新北师大版数学七年级（下）第六章《概率初步》单元检测卷 题型：单选题

    如图，在空白网格内将某一个小正方形涂成阴影部分，且所涂的小正方形与原阴影图形的小正方形至少有一边重合．小红按要求涂了一个正方形，所得到的阴影图形恰好是轴对称图形的概率为（ ）

    A． B． C． D．

    C． 【解析】 试题分析：如图所示：所涂的小正方形与原阴影图形的小正方形至少有一边重合的一共有9个， 能构成轴对称图形的有所标数据1，2，3，4，共4个，则所得到的阴影图形恰好是轴对称图形的概率为：． 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第四章　三角形 单元检验题 含答案 题型：填空题

    如图所示， AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3=_____.

    55° 【解析】求出∠BAD=∠EAC，证△BAD≌△EAC，推出∠2=∠ABD=30°，根据三角形的外角性质求出即可． 【解析】 ∵∠BAC=∠DAE， ∴∠BAC﹣∠DAC=∠DAE﹣∠DAC， ∴∠1=∠EAC， 在△BAD和△EAC中， AB=AC，∠BAD=∠EAC， ∴△BAD≌△EAC（SAS）， ∴∠2=∠ABD=30°， ∵...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第四章　三角形 单元检验题 含答案 题型：单选题

    在下列长度的四根木棒中，能与4cm、9cm长的两根木棒钉成一个三角形的是（　　）

    A. 4cm B. 5cm C. 9cm D. 13cm

    C 【解析】试题解析：根据三角形的三边关系，得：第三边应大于两边之差，且小于两边之和， 即9-4=5，9+4=13． ∴第三边取值范围应该为：5＜第三边长度＜13， 故只有C选项符合条件． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下5.3.2 线段垂直平分线的性质 同步练习 题型：单选题

    △ABC中，AB = 5，AC = 6，BC = 4，边AB的垂直平分线交AC于点D，则△BDC的周长是（ ）

    A. 8 B. 9 C. 10 D. 11

    C 【解析】试题分析：由ED是AB的垂直平分线，可得AD=BD，又由△BDC的周长=DB+BC+CD，即可得△BDC的周长=AD+BC+CD=AC+BC． ∵ED是AB的垂直平分线， ∴AD=BD， ∵△BDC的周长=DB+BC+CD， ∴△BDC的周长=AD+BC+CD=AC+BC=6+4=10．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版八年级数学下册 第一章 三角形的证明 1.2 直角三角形 同步训练卷 题型：解答题

    （2011•江津区）在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF．

    （1）求证：Rt△ABE≌Rt△CBF；

    （2）若∠CAE=30°，求∠ACF的度数．

    （1）见解析；（2）60°． 【解析】 试题分析：（1）由AB=CB，∠ABC=90°，AE=CF，即可利用HL证得Rt△ABE≌Rt△CBF； （2）由AB=CB，∠ABC=90°，即可求得∠CAB与∠ACB的度数，即可得∠BAE的度数，又由Rt△ABE≌Rt△CBF，即可求得∠BCF的度数，则由∠ACF=∠BCF+∠ACB即可求得答案． （1）证明：∵∠ABC=90°，...

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学九年级下册 第一章 直角三角形的边角关系 1.1 锐角三角函数 同步练习 题型：填空题

    如图，将以A为直角顶点的等腰Rt△ABC沿直线BC平移得到△A′B′C′，使点B′与C重合，连接A′B，则sin∠A′BC′的值为_____，cos∠A′BC＝________．

    【解析】过A′作出A′D⊥BC′，垂足为D， 在等腰直角三角形A′B′C′中，则A′D是底边上的中线， ∴B′C′=2 A′D， ∵BC=B′C′，BD=BC+B′D， ∴A′B= ， ∴ sin∠A′BC′=，cos∠A′BC＝， 故答案为： ， .

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册第二章《相交线与平行线》单元测试A 题型：填空题

    如图，(1)∵∠A=_____(已知)，

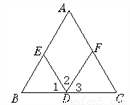
    ∴AC∥ED( )

    (2)∵∠2=_____(已知)，

    ∴AC∥ED( )

    (3)∵∠A+_____=180°(已知)，

    ∴AB∥FD( )

    (4)∵AB∥_____(已知)，

    ∴∠2+∠AED=180°( )

    (5)∵AC∥_____(已知)，

    ∴∠C=∠1( )

    (1)∠BED 同位角相等,两直线平行? (2)∠DFC 内错角相等，两直线平行? (3)∠AFD 同旁内角互补，两直线平行? (4)DF 两直线平行，同旁内角互补? (5)ED 两直线平行，同位角相等 【解析】(1)∠BED ,同位角相等,两直线平行? (2)∠DFC ,内错角相等，两直线平行? (3)∠AFD ,同旁内角互补，两直线平行? (4)...

    查看答案和解析>>

    同步练习册答案