
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源:数学人教版2019届九年级上册22.3 实际问题与二次函数(2) 同步训练 题型:单选题
有一座抛物线形拱桥,正常水位桥下面宽度为20米,拱顶距离水平面4米,如图建立直角坐标系,若正常水位时,桥下水深6米,为保证过往船只顺利航行,桥下水面宽度不得小于18米,则当水深超过多少米时,就会影响过往船只的顺利航行( )
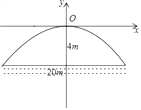
A. 2.76米 B. 6.76米 C. 6米 D. 7米
查看答案和解析>>
科目:初中数学 来源:数学2019届人教版九年级上册22.2.1 抛物线与x轴的交点 同步训练 题型:单选题
抛物线y=-2x2-x+2与坐标轴的交点个数是( )
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:初中数学 来源:2018-2019学年度人教版数学七年级上册一课一练:2.1.3 多项式 题型:单选题
在多项式6y3-4x5-8+2y4z2中,最高次项的系数和常数项分别为( )
A. 6和-8 B. -4和-8 C. 2和-8 D. -4和8
查看答案和解析>>
科目:初中数学 来源:人教版2019届九年级上册22.1.4 待定系数法求二次函数解析式同步训练 题型:解答题
已知二次函数的图象以A(﹣1,4)为顶点,且过点B(2,﹣5).
(1)求该函数的关系式;
(2)求当横坐标取﹣3和1时所对应的函数值;
(3)根据(2)计算,直接写出当x的值在什么范围时,所对应的函数值大于0.
查看答案和解析>>
科目:初中数学 来源:江苏省东台市第五联盟2018-2019学年八年级上学期第一次月考数学试卷 题型:解答题
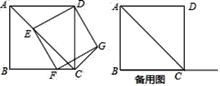
(题文)(问题引领)
问题1:在四边形ABCD中,CB=CD,∠B=∠ADC=90°,∠BCD=120°.E,F分别是AB,AD上的点.且∠ECF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结CG,先证明
△CBE≌△CDG,再证明△CEF≌△CGF.他得出的正确结论是________________.
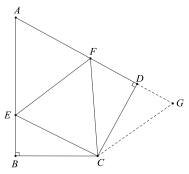
(探究思考)
问题2:若将问题1的条件改为:四边形ABCD中,CB=CD,∠ABC+∠ADC=180°,
∠ECF=  ∠BCD, 问题1的结论是否仍然成立?请说明理由.
∠BCD, 问题1的结论是否仍然成立?请说明理由.
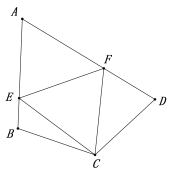
(拓展延伸)
问题3:在问题2的条件下,若点E在AB的延长线上,点F在DA的延长线上,则问题2的结论是否仍然成立?若不成立,猜测此时线段BE、DF、EF之间存在什么样的等量关系?并说明理由.
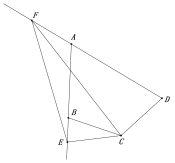
查看答案和解析>>
科目:初中数学 来源:江苏省东台市第五联盟2018-2019学年八年级上学期第一次月考数学试卷 题型:解答题
已知:如图点A、B、C、D在一条直线上,EA∥FB,EC∥FD,AB=CD,求证:EA=FB.

查看答案和解析>>
科目:初中数学 来源:山东省2019届九年级北师大版上册第一次月考数学试卷 题型:解答题
四边形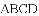
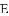
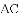
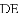
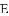
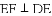
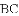
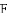
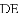
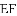
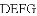
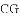
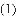
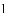
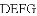
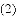
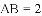
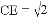 ,求
,求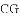
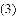
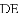
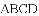
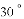 时,直接写出
时,直接写出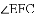
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com