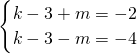关于x的方程kx2-(k-1)x+1=0有有理根,求整数k的值.
解:(1)当k=0时,x=-1,方程有有理根.
(2)当k≠0时,因为方程有有理根,
所以若k为整数,则△=(k-1)
2-4k=k
2-6k+1必为完全平方数,
即存在非负整数m,使k
2-6k+1=m
2.
配方得:(k-3+m)(k-3-m)=8,
由k-3+m和k-3-m是奇偶相同的整数,其积为8,
所以它们均是偶数.又k-3+m≥k-3-m.
从而
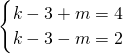
或
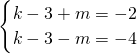
解得k=6或k=0(舍去),综合(1)(2),
所以方程kx
2-(k-1)x+1=0有有理根,整数k的值为0或6.
分析:先要讨论k的取值确定方程,(1)k=0,方程为一元一次方程,显然有有理根;(2)k≠0,方程为一元二次方程,要有理根,则△=(k-1)
2-4k=k
2-6k+1必为完全平方数,可设k
2-6k+1=m
2(m非负整数),变形为:(k-3+m)(k-3-m)=8,然后利用m,k都为整数,运用整数的性质,转化为两个二元一次方程组求解即可.
点评:本题考查了一元二次方程ax
2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△为完全平方数时,方程有两个有理数根;同时整数的奇偶性和整除的性质以及二元一次方程组的解法.

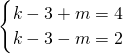 或
或