
在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.如图,已知⊙O的半径为5,则抛物线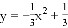 与该圆所围成的阴影部分(不包括边界)的整点个数是( )
与该圆所围成的阴影部分(不包括边界)的整点个数是( )
A. 24 B. 23 C. 22 D. 21
科目:初中数学 来源:山东省2017-2018学年八年级下学期期末模拟测试数学试卷 题型:单选题
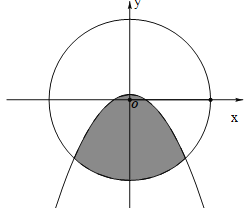
如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120° 的菱形,剪口与第二次折痕所成角的度数应为
A. 15°或30° B. 30°或45° C. 45°或60° D. 30°或60°
查看答案和解析>>
科目:初中数学 来源:2018-2019学年度浙教版数学七年级上册同步练习:2.7 近似数 题型:填空题
某种计算机每秒运算次数是4.66亿次,4.66亿次精确到_____位,4.66亿次用科学记数法可以表示为_____次.
查看答案和解析>>
科目:初中数学 来源:沪科版九年级上册数学第21章 二次函数与反比例函数 单元测试卷 题型:解答题
某公司生产A种产品,它的成本是6元/件,售价是8元/件,年销售量为5万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足我们学过的二种函数(即一次函数和二次函数)关系中的一种,它们的关系如下表:
x(万元) | 0 | 0.5 | 1 | 1.5 | 2 | … |
y | 1 | 1.275 | 1.5 | 1.675 | 1.8 | … |
(1)求y与x的函数关系式(不要求写出自变量的取值范围)
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润W(万元)与广告费用x(万元)的函数关系式,并计算每年投入的广告费是多少万元时所获得的利润最大?
(3)如果公司希望年利润W(万元)不低于14万元,请你帮公司确定广告费的范围.
查看答案和解析>>
科目:初中数学 来源:沪科版九年级上册数学第21章 二次函数与反比例函数 单元测试卷 题型:填空题
竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t= .
查看答案和解析>>
科目:初中数学 来源:沪科版九年级上册数学第21章 二次函数与反比例函数 单元测试卷 题型:单选题
二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中,x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 |
y | 0 | ﹣3 | ﹣4 | ﹣3 |
下列结论:
①ac<0;
②当x>1时,y随x的增大而增大;
③﹣4是方程ax2+(b﹣4)x+c=0的一个根;
④当﹣1<x<0时,ax2+(b﹣1)x+c+3>0.其中正确结论的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源:2018-2019学年人教版数学九年级上册 第22章《二次函数》 单元测试卷 题型:解答题
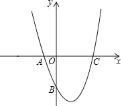
如图,已知抛物线y=(x﹣1)2+k的图象与x轴交于点A(﹣1,0),C两点,与y轴交于点B.
(1)求抛物线解析式及B点坐标;
(2)在抛物线上是否存在点P使S△PAC= S△ABC?若存在,求出P点坐标,若不存在,请说明理由;
S△ABC?若存在,求出P点坐标,若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形,若存在,求出Q点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2018-2019学年人教版数学九年级上册 第22章《二次函数》 单元测试卷 题型:单选题
如图所示,已知一次函数y= x+c的图象如图,则二次函数y=ax2+bx+c在平面直角坐标系中的图象可能是( )
x+c的图象如图,则二次函数y=ax2+bx+c在平面直角坐标系中的图象可能是( )
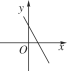
A. 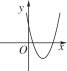 B.
B. 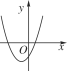 C.
C. 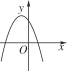 D.
D. 
查看答案和解析>>
科目:初中数学 来源:2018年秋人教版九年级上册数学 期末检测卷 题型:解答题
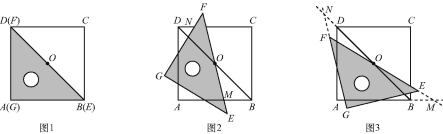
如图1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)如图2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想.
(2)若三角尺GEF旋转到如图3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com