
 x2+
x2+ x+2 ��x����A��B���㣬��y���ڵ�C��
x+2 ��x����A��B���㣬��y���ڵ�C��
��: ��1������y=- x2+
x2+ x+2
x+2
��y=0ʱ, y=- x2+
x2+ x+2=0�� ���x1=-1, x2=4
x+2=0�� ���x1=-1, x2=4
��x=0ʱ, y=2
��A��B��C���������ֱ�Ϊ A��-1,0��,B��4,0��,C��0,2��
��OA=1��OB= 4��OC=2�� ��AB=OA+OB=5����AB2=25
��Rt��AOC��AC2=OA2+OC2=12+22=5
��Rt��COB��BC2=OC2+OB2=22+42=20
��AC2+BC2=AB2
���ABC���ԡ�ACBΪֱ�ǵ�ֱ�������Ρ�
��2���⣺��ֱ��DE�Ľ���ʽΪֱ��x=m����OD= m��DE��OB
��OC��AB����OC��DE�����BDE�ס�BOC ��
��OC=2��OB=4��BD=OB-OD=4-m����DF=
��EF=DFʱ��DE=2DF=4-m����E�������Ϊ��m, 4-m��
��E����������
���m1=1��m2=4. ��0��m��4����m2=4��ȥ�� �൱m=1ʱ��EF=DF
��3���⣺С��ͬѧ�Ĺ۵��Ǵ����
��OD= m, DE��OB�� E����������
��E�������ɱ�ʾΪ
��DE=- m2+
m2+ m+2
m+2
��DF=2- m����EF=DE-DF=-
m����EF=DE-DF=- m 2+2m
m 2+2m
��S��BCE=S��CEF+S��BEF= EF��OD+
EF��OD+ EF��BD=
EF��BD= EF����OD+BD�� =
EF����OD+BD�� = EF��OB=
EF��OB= EF��4=2EF
EF��4=2EF
��S��BCE=-m 2+4m=-��m2-4m+4-4��=-��m-2��2+4
�൱m=2ʱ, S��BCE�����ֵ,��BCE��������Ϊ4
�ߵ�m=2ʱ,- m 2+
m 2+ m+2=3����E���������2, 3��
m+2=3����E���������2, 3��
��������y=- x2+
x2+ x+2�Ķ�������Ϊ��
x+2�Ķ�������Ϊ�� ��
�� ������С��ͬѧ�Ĺ۵��Ǵ���� ��
������С��ͬѧ�Ĺ۵��Ǵ���� ��


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
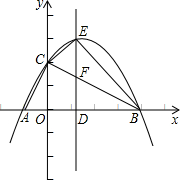 ��ͼƽ��ֱ������ϵ�У�������y=-
��ͼƽ��ֱ������ϵ�У�������y=-| 1 |
| 2 |
| 3 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| k | x |
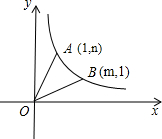 OA��OB��
OA��OB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ����ͼƽ��ֱ������ϵ�У���ABC��������A��B��C������ֱ�ΪA��2��-1����B��1��-3����C��4��-4����
����ͼƽ��ֱ������ϵ�У���ABC��������A��B��C������ֱ�ΪA��2��-1����B��1��-3����C��4��-4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ����ͼƽ��ֱ������ϵ�л�������y=-
����ͼƽ��ֱ������ϵ�л�������y=-| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 19����֪����ͼƽ��ֱ������ϵ�У���ABC������������ֱ�ΪA��-3��-2����B��-5��0����C��-2��4����
19����֪����ͼƽ��ֱ������ϵ�У���ABC������������ֱ�ΪA��-3��-2����B��-5��0����C��-2��4�����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com