
求证:各边相等的圆的内接多边形是正多边形.
科目:初中数学 来源:1+1轻巧夺冠·优化训练·九年级数学下(北京课改版)·银版 题型:044
某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行如下讨论:
甲同学:这种多边形不一定是正多边形,如圆内接矩形;
乙同学:我发现边数是6时,它也不一定是正多边形.如图一,△ABC是正三角形,AD=BE=CF,可以证明六边形ADBECF的各内角相等,但它未必是正六边形;
丙同学:我能证明,边数是5时,它是正多边形.我想,边数是7时,它可能也是正多边形.
(1)请你说明乙同学构造的六边形各内角相等.
(2)请你证明,各内角都相等的圆内接七边形ABCDEFG(如图二)是正七边形(不必写已知、求证).
(3)根据以上探索过程,提出你的猜想(不必证明).

查看答案和解析>>
科目:初中数学 来源:2006年江苏省扬州市中考数学模拟试卷(一)(解析版) 题型:解答题
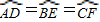 ,证明六边形ADBECF的各内角相等,但它未必是正六边形.
,证明六边形ADBECF的各内角相等,但它未必是正六边形.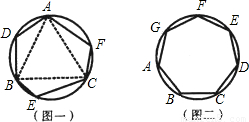
查看答案和解析>>
科目:初中数学 来源:2004年云南省中考数学试卷(解析版) 题型:解答题
 ,证明六边形ADBECF的各内角相等,但它未必是正六边形.
,证明六边形ADBECF的各内角相等,但它未必是正六边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com