
科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级下学期期末考试数学试卷 题型:解答题
解下列方程:
(1)x2﹣x﹣1=0(配方法) (2)3(x﹣1)2=x(x﹣1)
查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018年中考数学试卷 题型:单选题
下列运算正确的是( )
A. a2+a3=a5 B. (a2)3=a5 C. a4﹣a3=a D. a4÷a3=a
查看答案和解析>>
科目:初中数学 来源:北师大版八年级数学下册期末单元测试卷:第二章 一元一次不等式与一元一次不等式组 题型:单选题
不等式组 的解集是( )
的解集是( )
A. x≤2 B. x>1 C. 1<x≤2 D. 无解
查看答案和解析>>
科目:初中数学 来源:山东省聊城市2018年中考数学试卷 题型:解答题
如图,已知抛物线 与
与

































(1)求出这条抛物线的表达式;
(2)当
 的值;
的值;
(3)当矩形





查看答案和解析>>
科目:初中数学 来源:山东省聊城市2018年中考数学试卷 题型:填空题
用一块圆心角为216°的扇形铁皮,做一个高为40cm的圆锥形工件(接缝忽略不计),那么这个扇形铁皮的半径是_____cm.
查看答案和解析>>
科目:初中数学 来源:山西省2018届数学中考信息冲刺卷 题型:解答题
数学活动
问题情境:
如图1,在∆ABC中,AB=AC,∠BAC=90°,D,E分别是边AB,AC的中点,将∆ADE绕点A顺时针旋转α角(0°<α<90°)得到∆AD′E′,连接CE′,BD′.探究CE′与BD′的数量关系;
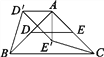 图1
图1 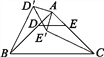 图2
图2 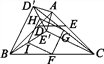 图3
图3 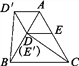 图4
图4
探究发现:
(1)图1中,CE′与BD′的数量关系是________;
(2)如图2,若将问题中的条件“D,E分别是边AB,AC的中点”改为“D为AB边上任意一点,DE∥BC交AC于点E”,其他条件不变,(1)中CE′与BD′的数量关系还成立吗?请说明理由;
拓展延伸:
(3)如图3,在(2)的条件下,连接BE′,CD′,分别取BC,CD′,E′D′,BE′的中点F,G,H,I,顺次连接F,G,H,I得到四边形FGHI.请判断四边形FGHI的形状,并说明理由;
(4)如图4,在∆ABC中,AB=AC,∠BAC=60°,点D,E分别在AB,AC上,且DE∥BC,将∆ADE绕点A顺时针旋转60°得到∆AD′E′,连接CE′,BD′.请你仔细观察,提出一个你最关心的数学问题(例如:CE′与BD′相等吗?).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com