
已知x1,x2是方程x2﹣2x﹣1=0的两个根,则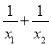 等于_____.
等于_____.
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:解答题
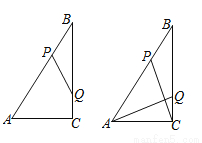
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)当t为何值时,四边形ACQP的面积最小,最小值是多少?
(3)连接AQ,CP,若AQ⊥CP,求t的值.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:单选题
有一长、宽、高分别为5cm、4cm、3cm的木箱,在它里面放入一根细木条(木条的粗细、形变忽略不计)要求木条不能露出木箱.请你算一算,能放入的细木条的最大长度是( )
A. 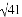 cm B.
cm B. 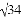 cm C.
cm C. 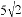 cm D.
cm D. 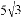 cm
cm
查看答案和解析>>
科目:初中数学 来源:北师大版九年级上册4.7三角形相似专题--高的比等于相似比 题型:单选题
有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
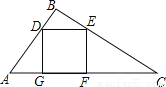
A. 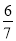 B.
B. 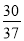 C.
C. 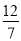 D.
D. 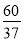
查看答案和解析>>
科目:初中数学 来源:广东省2017届九年级上学期第二次月考数学试卷 题型:解答题
先化简,再求值: 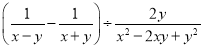 ,其中x=1+
,其中x=1+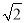 ,y=1﹣
,y=1﹣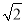 .
.
查看答案和解析>>
科目:初中数学 来源:广东省2017届九年级上学期第二次月考数学试卷 题型:单选题
如图,若一次函数y=ax+b的图象经过二、三、四象限,则二次函数y=ax2+bx的图象可能是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:广东省2017届九年级上学期第二次月考数学试卷 题型:单选题
函数y=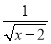 中自变量x的取值范围是( )
中自变量x的取值范围是( )
A. x>2 B. x<2 C. x≠2 D. x≥2
A 【解析】试题分析:根据分母不能为零,被开方数不能为负数得:x-2>0,所以x>2.故选A.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:单选题
如图,扇形AOB 中,半径OA=2,∠AOB=120°,C 是弧AB的中点,连接AC、BC,则图中阴影部分面积是 ( )
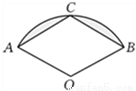
A. 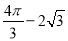 B.
B. 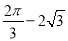
C. 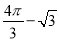 D.
D. 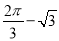
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(1)练习 题型:填空题
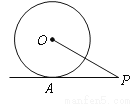
如图,PA是⊙O的切线,切点为A,PA=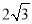 ,∠APO=30°,则
,∠APO=30°,则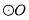 的半径长为______.
的半径长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com