解:(1)连接BF,
∵AB为⊙O的直径,
∴∠AFB=90°,
∵四边形ABCD是正方形,
∴AC⊥BD,
∴点B,F,D共线,
即点F是对角线AC与BD的交点,
∴∠ABF=45°,
∴∠AEF=∠ABF=45°;
(2)连接BE,
∵AB是直径,
∴∠AEB=90°,
∵AB=8,AE=7,
∴sin∠ABE=

=

,
∵∠ABE=∠AFE,
∴∠AFE的正弦值为

;
(3)连接OF,
∵四边形ABCD是正方形,
∴AF=BF,
∵OA=OB,
∴OF⊥AB,
即∠BOF=90°,
∴S
阴影=S
梯形OBCF-S
扇形BOF=

×(OF+BC)×OB-

π×(OB)
2=

×(4+8)×4-

×π×16=24-4π.
∴阴影部分的面积为24-4π.
分析:(1)首先连接BF,易得即点F是对角线AC与BD的交点,即可得∠ABF=45°,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可求得∠AEF的度数;
(2)首先连接BE,由AB是直径,即可得∠AEB=90°,然后在Rt△ABE中,由三角函数的定义,即可求得∠ABE的正弦值,继而求得∠AFE的正弦值;
(3)连接OF,由S
阴影=S
梯形OBCF-S
扇形BOF,即可求得答案.
点评:此题考查了正方形的性质、圆周角定理、三角函数的定义以及扇形的面积.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

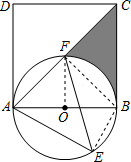
 如图,已知正方形ABCD的边长为8,以AB为直径的⊙O交对角线AC于点F,点E在⊙O上(E,F分别在直径AB的两侧).
如图,已知正方形ABCD的边长为8,以AB为直径的⊙O交对角线AC于点F,点E在⊙O上(E,F分别在直径AB的两侧).
 =
= ,
, ;
;  ×(OF+BC)×OB-
×(OF+BC)×OB- π×(OB)2=
π×(OB)2= ×(4+8)×4-
×(4+8)×4- ×π×16=24-4π.
×π×16=24-4π.

 阅读快车系列答案
阅读快车系列答案 (2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点. 如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上. 如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.