解:由a
2+b
2-6ab=0得:a
2+2ab+b
2-8ab=0,
即(a+b)
2=8ab,又a>b>0,
所以a+b=

=2
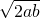
;
又由a
2+b
2-6ab=0得:a
2-2ab+b
2-4ab=0,
即(a-b)
2=4ab,又a>b>0,
所以a-b=

=2

,
则

=-

=-

=-

.
分析:把已知等式的-6ab变为2ab-8ab,利用加法的交换律及结合律使之能用完全平方公式,然后根据a与b都大于0,开方即可表示出a+b;把-6ab变为-2ab-4ab,同理结合后,根据a大于b,且a与b都大于0,开方即可表示出a-b,然后把所求的式子提取-1后,将表示出的a+b及a-b代入,化简即可求出值.
点评:此题考查了分式的化简求值,以及完全平方公式的运用.重点要理解完全平方公式的结构特点:两数的平方和及两数积的2倍等于两数和的平方,利用“拆项法”灵活变换题中的“-6ab”.

 的值.
的值. =2
=2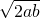 ;
; =2
=2 ,
, =-
=- =-
=- =-
=- .
.

 名师指导一卷通系列答案
名师指导一卷通系列答案