
 如图,顶点为D的抛物线y=x2+bx-3与x轴相交于A、B两点,与y轴相交于点C,连结BC,已知△BOC是等腰三角形.
如图,顶点为D的抛物线y=x2+bx-3与x轴相交于A、B两点,与y轴相交于点C,连结BC,已知△BOC是等腰三角形. 解:(1)令y=x2+bx-3中x=0,得到y=-3,即C(0,-3),OC=3,
解:(1)令y=x2+bx-3中x=0,得到y=-3,即C(0,-3),OC=3, ×1×3+
×1×3+ ×2×4+
×2×4+ ×(3+4)×1=9.
×(3+4)×1=9.

科目:初中数学 来源: 题型:
 (2013•湖州)如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为3
(2013•湖州)如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为3| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一个隧道的横截面成抛物线形,它的底部宽12米、高6米.车辆在此隧道可以双向通行,但规定车辆必须在隧道的中心线右侧、距离路边缘2米这一范围内行驶,并保持车辆顶部与隧道的空隙不少于
如图,一个隧道的横截面成抛物线形,它的底部宽12米、高6米.车辆在此隧道可以双向通行,但规定车辆必须在隧道的中心线右侧、距离路边缘2米这一范围内行驶,并保持车辆顶部与隧道的空隙不少于| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
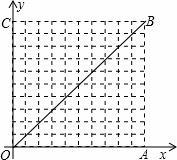
如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为![]() ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
|
| A. | 16 | B. | 15 | C. | 14 | D. | 13 |
查看答案和解析>>
科目:初中数学 来源:2013年海南省海口市中考数学模拟试卷(九)(解析版) 题型:解答题
 米.
米.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(浙江湖州卷)数学(解析版) 题型:选择题
如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为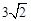 ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是
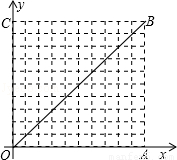
A.16 B.15 C.14 D.13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com