
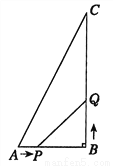
如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,设移动时间为t(s).
(1)当t=2时,求△PBQ的面积;
(2)当t为多少时,四边形APQC的面积最小?最小面积是多少?
(3)当t为多少时,△PQB与△ABC相似.
科目:初中数学 来源:四川省遂宁市2017-2018学年八年级上学期教学水平监测数学试卷 题型:填空题
一个正数的平方根是2x+2与-x-5,则这个正数是__________.
64 【解析】由题意得:查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古呼伦贝尔市七年级(下)期中数学试卷 题型:单选题
如图,能判定EB∥AC的条件是( )
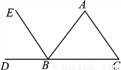
A. ∠C=∠ABE B. ∠A=∠EBD C. ∠C=∠ABC D. ∠A=∠ABE
B 【解析】在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角,被判断平行的两直线是否由“三线八角”而产生的被截直线,因此: A、∠C=∠ABE不能判断出EB∥AC,故A选项不符合题意; B、∠A=∠EBD不能判断出EB∥AC,故B选项不符合题意; C、∠C=∠ABC只能判断出AB=AC,不能判断出EB∥AC,故C选项不符合题意; D、∠A=∠ABE,...查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版八年级数学下册 期中测评 题型:填空题
已知等腰三角形的一个内角是80°,则它的底角的度数是_______.
50°或80° 【解析】分两种情况: ①当80°的角为等腰三角形的顶角时, 底角的度数=(180°?80°)÷2=50°; ②当80°的角为等腰三角形的底角时,其底角为80°, 故它的底角度数是50或80. 故答案为:80°或50°.查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版八年级数学下册 期中测评 题型:单选题
在如图所示的方格纸中,△ABC经过变换得到△DEF,正确的变换是( )
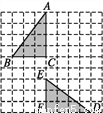
A. 把△ABC绕点C逆时针方向旋转90°,再向下平移2格
B. 把△ABC绕点C顺时针方向旋转90°,再向下平移5格
C. 把△ABC向下平移4格,再绕点C逆时针方向旋转180°
D. 把△ABC向下平移5格,再绕点C顺时针方向旋转180°
B 【解析】试题分析:几何变换只改变图形的位置,不改变图形的形状与大小,观察图象可知,C与F,A与D,B与E分别是对应点,由长度可知AC与DF,EF与BC,AB与DE是对应边,∴先把△ABC绕点C顺时针方向旋转90°,再向下平移5格即可得到△DEF.故选B.查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2018届九年级上学期教学水平监测数学试卷 题型:解答题
已知关于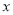 的方程
的方程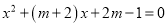 .
.
(1)求证:方程有两个不相等的实数根.
(2)当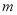 为何值时,方程的两根互为相反数?并求出此时方程的解.
为何值时,方程的两根互为相反数?并求出此时方程的解.
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2018届九年级上学期教学水平监测数学试卷 题型:填空题
在二次根式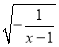 中
中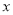 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2018届九年级上学期教学水平监测数学试卷 题型:单选题
若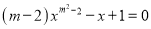 是一元二次方程,则m的值为
是一元二次方程,则m的值为
A. ±2 B. 2 C. -2 D. 以上都不对
C 【解析】试题解析:根据题意得: , 解得:m=-2. 故选C.查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期中测评试卷 题型:填空题
如图是一张宽为m的矩形台球桌ABCD,一球从点M(点M在长边CD上)出发沿虚线MN射向边BC,然后反弹到边AB上的点P.如果MC=n,∠CMN=α,那么点P与点B的距离为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com