
已知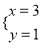 和
和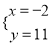 都是ax+by=7的解,则a=____,b=_____.
都是ax+by=7的解,则a=____,b=_____.
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源:2018人教版八年级数学下册练习:第二十章达标检测卷 题型:单选题
期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,小明说:“我们组成绩是86分的同学最多”,小英说:“我们组的7位同学成绩排在最中间的恰好也是86分”.上面两位同学的话能反映出的统计量分别是( )
A. 众数和平均数 B. 平均数和中位数
C. 众数和方差 D. 众数和中位数
D 【解析】一组数据中出现次数最多的数值是众数;将数据从小到大排列,当项数为奇数时中间的数为中位数,当项数为偶数时中间两个数的平均数为中位数;由题可知,小明所说的是多数人的分数,是众数,小英所说的为排在中间人的分数,是中位数. 故选为D.查看答案和解析>>
科目:初中数学 来源:江苏省苏州市姑苏区2017~2018学年第一学期八年级数学期末考试试卷 题型:解答题
解下列分式方程:
(1) (2)
(2) .
.
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市姑苏区2017~2018学年第一学期八年级数学期末考试试卷 题型:单选题
下列图案属于轴对称图形的是( )
A.  B.
B.  C.
C. 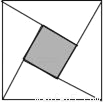 D.
D. 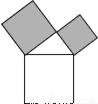
查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第八章达标检测卷 题型:解答题
已知y=3xy+x,求代数式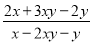 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第八章达标检测卷 题型:单选题
若 是方程
是方程 的解,则(a+b)·(a-b)的值为( )
的解,则(a+b)·(a-b)的值为( )
A.  B.
B.  C. -16 D. 16
C. -16 D. 16
查看答案和解析>>
科目:初中数学 来源:广东省潮州市潮安区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:解答题
如图,己知△ABC是等边三角形,点P在△ABC内,点Q在△ABC外,分别连接AP、BP、AQ、CQ,∠ABP=∠ACQ, BP=CQ.
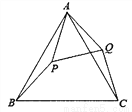
(1)求证:△ABP≌△ACQ;
(2)连接PQ,求证△APQ是等边三角形;
(3)连接P设△CPQ是以 PQC为顶角的等腰三角形,且∠BPC=100
PQC为顶角的等腰三角形,且∠BPC=100 ,求∠APB的度数.
,求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源:广东省潮州市潮安区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:单选题
在公式 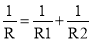 中,己知R1=3,R2=2,则( )
中,己知R1=3,R2=2,则( )
A. R=5 B. R=l.5 C. R=l.2 D. R=l
C 【解析】∵R1=3,R2=2, ∴=, ∴. 故选C.查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期九年级期末统一考试数学试卷 题型:填空题
如图,一段抛物线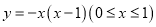 记为
记为 ,它与
,它与 轴的交点为
轴的交点为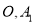 ,顶点为
,顶点为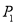 ;将
;将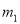 绕点
绕点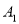 旋转180°得到
旋转180°得到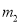 ,交
,交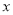 轴于点为
轴于点为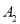 ,顶点为
,顶点为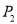 ;将
;将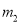 绕点
绕点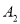 旋转180°得到
旋转180°得到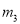 ,交
,交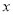 轴于点为
轴于点为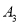 ,顶点为
,顶点为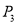 ;……,如此进行下去,直至到
;……,如此进行下去,直至到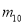 ,顶点为
,顶点为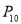 ,则顶点
,则顶点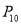 的坐标为 _________ .
的坐标为 _________ .
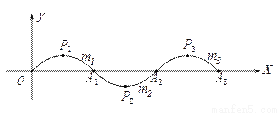
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com