
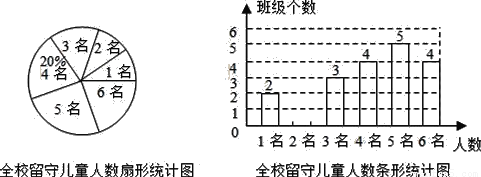
为了解外来务工子女就学情况,某校对七年级各班级外来务工子女的人数情况进行了统计,发现各班级中外来务工子女的人数有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅统计图:
(1)求该校七年级平均每个班级有多少名外来务工子女?并将该条形统计图补充完整;
(2)学校决定从只有2名外来务工子女的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名外来务工子女来自同一个班级的概率.
科目:初中数学 来源:湖北省武汉市洪山区2018届九年级(上)期中数学试卷 题型:填空题
一次会议上,每两个参加会议的人都相互握一次手,有人统计一共握了36次手,设到会的人数为x人,则根据题意列方程为_____.
x(x﹣1)=36 【解析】试题解析:设到会的人数为x人,则每个人握手(x﹣1)次, 由题意得, x(x﹣1)=36, 故答案是: x(x﹣1)=36.查看答案和解析>>
科目:初中数学 来源:四川省西昌市2017-2018学年九年级数学(上)期末模拟试卷 题型:解答题
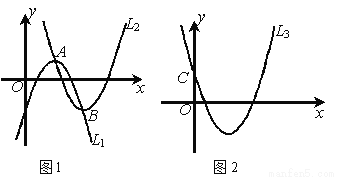
如图1,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上(点A与点B不重合),我们定义:这样的两条抛物L1,L2互为“友好”抛物线,可见一条抛物线的“友好”抛物线可以有多条.
(1)如图2,已知抛物线L3:y=2x2-8x+4与y轴交于点C,试求出点C关于该抛物线对称轴对称的点D的坐标;
(2)请求出以点D为顶点的L3的友好抛物线L4的解析式,并指出L3与L4中y同时随x增大而增大的自变量的取值范围;
(3)若抛物y=a1 (x-m) 2+n的任意一条友好抛物线的解析式为y=a2 (x-h) 2+k,请写出a1与a2的关系式,并说明理由.
查看答案和解析>>
科目:初中数学 来源:四川省西昌市2017-2018学年九年级数学(上)期末模拟试卷 题型:填空题
一元二次方程x2=x的解为_____.
x1=0,x2=1 【解析】试题分析:首先把x移项,再把方程的左面分解因式,即可得到答案. 试题解析:移项得:x2-x=0, ∴x(x-1)=0, x=0或x-1=0, ∴x1=0,x2=1.查看答案和解析>>
科目:初中数学 来源:重庆市2018届2017年秋期期末冲刺卷 题型:解答题
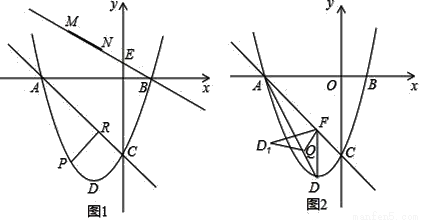
如图1,已知抛物线y=x2+2x﹣3与x轴相交于A,B两点,与y轴交于点C,D为顶点.
(1)求直线AC的解析式和顶点D的坐标;
(2)已知E(0, 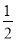 ),点P是直线AC下方的抛物线上一动点,作PR⊥AC于点R,当PR最大时,有一条长为
),点P是直线AC下方的抛物线上一动点,作PR⊥AC于点R,当PR最大时,有一条长为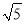 的线段MN(点M在点N的左侧)在直线BE上移动,首尾顺次连接A、M、N、P构成四边形AMNP,请求出四边形AMNP的周长最小时点N的坐标;
的线段MN(点M在点N的左侧)在直线BE上移动,首尾顺次连接A、M、N、P构成四边形AMNP,请求出四边形AMNP的周长最小时点N的坐标;
(3)如图2,过点D作DF∥y轴交直线AC于点F,连接AD,Q点是线段AD上一动点,将△DFQ沿直线FQ折叠至△D1FQ,是否存在点Q使得△D1FQ与△AFQ重叠部分的图形是直角三角形?若存在,请求出AQ的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:重庆市2018届2017年秋期期末冲刺卷 题型:填空题
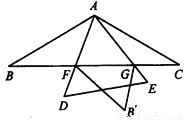
如图, 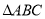 中,
中, 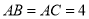 ,
, 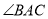 =120°,以
=120°,以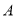 为一个顶点的等边三角形
为一个顶点的等边三角形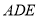 绕点A在
绕点A在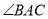 内旋转,
内旋转, 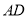 、
、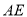 所在的直线与
所在的直线与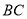 边分别交于点
边分别交于点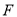 、
、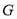 ,若点
,若点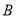 关于直线
关于直线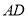 的对称点为
的对称点为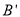 ,当
,当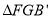 是以点
是以点 为直角顶点的直角三角形时,
为直角顶点的直角三角形时, 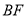 的长为__
的长为__
查看答案和解析>>
科目:初中数学 来源:重庆市2018届2017年秋期期末冲刺卷 题型:单选题
如图,一圆内切于四边形ABCD,AB=16,CD=10,则四边形ABCD的周长为( )
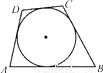
A. 50 B. 52 C. 54 D. 56
B 【解析】试题解析:根据切线长定理,可以证明圆外切四边形的性质:圆外切四边形的两组对边的和相等, 所以四边形的周长为: 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初一上期中数学试卷数学试卷 题型:填空题
观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a+b+c的值为 .
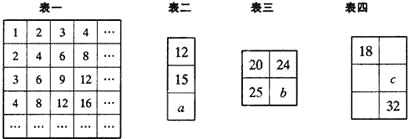
查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2016-2017学年度上学期期末考试七年级数学试卷 题型:解答题
仔细阅读下列材料.
“分数均可化为有限小数或无限循环小数”,反之“有限小数或无限循环小数均可化为分数”.
例如: 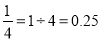
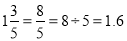
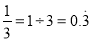
反之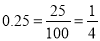
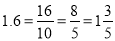
那么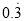 怎么化成
怎么化成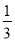 呢?
呢?
解:∵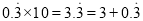
∴不妨设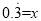 ,则上式变为10x=3+x,解得x=
,则上式变为10x=3+x,解得x=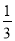 即
即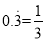 .
.
根据以上材料,回答下列问题:
(1)将分数化为小数: 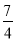 =_________,
=_________,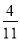 =_________;
=_________;
(2)将小数化为分数: 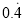 =_________,
=_________,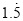 =_________;
=_________;
(3)将小数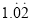
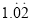 化为分数,需要写出推理过程.
化为分数,需要写出推理过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com