10名棋手参加比赛,规定:每两名棋手间都要比赛一次,胜者得2分,下和各得1分,输者得0分.比赛结果表明:棋手们所得分数各不相同,前两名棋手没输过,前两名的总分之和比第三名多20分,第四名得分与后四名得分总和相等,那么前六名得分分别是多少?
解:设第k名选手的得分为a
k(1≤k≤10),依题意得:a
1>a
2>a
3>…a
9>a
10a
1≤1+2×(9-1)=17,
a
2≤a
1-1=16,
a
3+20=a
1+a
2,
∴a
3≤13 ①,
又后四名棋手相互之间要比赛

=6场,每场比赛双方的得分总和为2分,
∴a
7+a
8+a
9+a
10≥12,
∴a
4≥12
而a
3≥a
4+1≥13,②
∴由①②得:a
3=13,
∴a
1+a
2=33,
∴a
1=17,a
2=16,
又∵a
1≤a
3-1=12,
∴a
4=12,
∵a
1+a
2+a
3+…a
8+a
9+a
10=
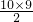
×2=90,
∴17+16+13+12+a
5+a
6+12=90,
而a
5+a
6≤a
5+a
5-1,
即:a
5≥10

,
又a
5<a
4=12,
∴a
5=11,a
6=9,
故前六名得分分别是:17,16,13,12,11,9.
分析:先设第k名选手的得分为a
k(1≤k≤10),得出a
1、a
2的值,再根据得出a
4≥12,求出a
3,再根据a
1≤a
3-1=12,求出a
4,最后根据a
1+a
2+a
3+…a
8+a
9+a
10=90分别求出a
5、a
6的值.
点评:本题考查了推理与论证;解决问题的关键是读懂题意,找到所求的量的等量关系是解题的关键.

 =6场,每场比赛双方的得分总和为2分,
=6场,每场比赛双方的得分总和为2分,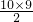 ×2=90,
×2=90, ,
,
