
 与x轴交于点B,与y轴交于点A.
与x轴交于点B,与y轴交于点A. ?若存在,请直接写出点E的坐标;若不存在,请说明理由.
?若存在,请直接写出点E的坐标;若不存在,请说明理由.
 (1)令x=0,y=6,令y=0,x=8,
(1)令x=0,y=6,令y=0,x=8, ),
), ,
, ,
, |b|,
|b|, a),
a), |9a-24|,
|9a-24|, |9a-24|=a,
|9a-24|=a, 或b=6
或b=6 时,b=
时,b=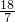 ,
, 或(6,-9).
或(6,-9). ),列出含有a的△MON的面积的表达式,根据二次函数的性质,求出其最值;
),列出含有a的△MON的面积的表达式,根据二次函数的性质,求出其最值;

科目:初中数学 来源: 题型:
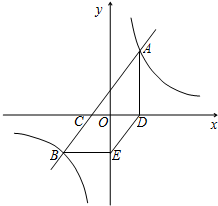 如图,已知直线AB与x轴交于点C,与双曲线y=
如图,已知直线AB与x轴交于点C,与双曲线y=| k |
| x |
| 20 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
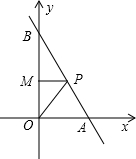 )是折线O→A→B上的动点(不与O点、B点重合),连接OP,MP,设△OPM的面积为S.
)是折线O→A→B上的动点(不与O点、B点重合),连接OP,MP,设△OPM的面积为S.查看答案和解析>>
科目:初中数学 来源:2011-2012年河北省藁城中学八年级上学期12月月考数学试卷(带解析) 题型:解答题
如图,已知直线AB与x轴交于A(6,0)点,与y轴交于B(0,10)点,点M的坐标为(0,4),点P(x,y)是折线O→A→B的动点(不与O点、B点重合),连接OP、MP,设△OPM的面积为S.
(1) 求S关于x的函数表达式,并写x的取值范围;
(2) 当△OPM是以OM为底边的等腰三角形时,求S的值;
(3) 当线段MP分△OAB的面积比为1∶4时,求P点坐标.
查看答案和解析>>
科目:初中数学 来源:2012年湖南省郴州市临武县楚江中学中考数学模拟试卷(二)(解析版) 题型:解答题
 交于A(3,
交于A(3, )、B(-5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.
)、B(-5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.
查看答案和解析>>
科目:初中数学 来源:2013届河北宣化二中八年级上学期期末数学试卷(解析版) 题型:解答题
如图,已知直线AB与x轴交于A(6,0)点,与y轴交于B(0,10)点,点M的坐标为(0,4),
点P(x,y)是折线O→A→B的动点(不与O点、B点重合),连接OP、MP,设△OPM的面积为S.
(1) 求S关于x的函数表达式,并写x的取值范围;
(2) 当△OPM是以OM为底边的等腰三角形时,求S的值;
(3) 当线段MP分△OAB的面积比为1∶4时,求P点坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com