
 如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=
如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=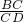 ;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是
;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是 =
=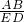 =
=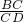 ;然后由直角三角形中的正切函数,得tan∠AEC=
;然后由直角三角形中的正切函数,得tan∠AEC= ,再由等量代换求得tan∠AEC=
,再由等量代换求得tan∠AEC=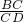 ;
; 解:∵△ABC和△CDE均为等腰直角三角形,
解:∵△ABC和△CDE均为等腰直角三角形, =
=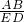 =
=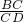
 ,
,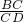 ;故本选项正确;
;故本选项正确; a2,S△CDE=
a2,S△CDE= b2,S梯形ABDE=
b2,S梯形ABDE= (a+b)2,
(a+b)2, S△ABC+S△CDE=
S△ABC+S△CDE= (a2+b2)≥ab(a=b时取等号),
(a2+b2)≥ab(a=b时取等号), (AB+ED)=
(AB+ED)= (BC+CD),
(BC+CD),

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

| BG | CG |
查看答案和解析>>
科目:初中数学 来源: 题型:
 10、如图,△ABC和△ADE都是等腰直角三角形,∠ACB和∠AED都是直角,点C在AD上,如果△ABC经旋转后能与△ADE重合,那么点
10、如图,△ABC和△ADE都是等腰直角三角形,∠ACB和∠AED都是直角,点C在AD上,如果△ABC经旋转后能与△ADE重合,那么点查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,BC=3,CD=1.
如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,BC=3,CD=1.| BC | CD |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交 CE于点G,连接BE.下列结论中:
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交 CE于点G,连接BE.下列结论中:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.
如图,△ABC和△ADE都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.| 2 |
| 10 |
| 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com