

(1)四边形ADEF是什么四边形?
(2)当△ABC满足什么条件时,四边形ADEF是矩形?
(3)当△ABC满足什么条件时,以A、D、E、F为顶点的四边形不存在?
| (1)∵△BCE、△ABD是等边三角形
∴∠DBA=∠EBC=60°,AB=BD,BE=BC ∴∠DBE=∠ABC,∴△DBE≌△ABC ∴DE=AC 又△ACF是等边三角形 ∴AC=AF,∴DE=AF 同理可证:AD=EF ∴四边形ADEF是平行四边形. (2)假设四边形ADEF是矩形 则∠DAF=90° 又∠DAB=∠FAC=60° ∠DAB+∠FAC+∠DAF+∠BAC=360° ∴∠BAC=150° 因此当△ABC中的∠BAC=150°时,四边形ADEF是矩形. (3)由图知道:∠DAB+∠FAC+∠DAF+∠BAC=360° 所以:当∠BAC=60°时,D、A、F为同一直线,与E点构不成四边形,即以A、D、E、F为顶点的四边形不存在. 结果:(1)四边形ADEF是平行四边形. (2)当△ABC中的∠BAC=150°时,四边形ADEF是矩形. (3)当△ABC中的∠BAC=60°时,以A、D、E、F为顶点的四边形不存在. |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 已知,如图,△ABC中,∠B=90°,BC=4cm,AC+AB=2BC,O是BC上一点,以O为圆心、OB为半径的圆与AC切于点D,交BC于点E.
已知,如图,△ABC中,∠B=90°,BC=4cm,AC+AB=2BC,O是BC上一点,以O为圆心、OB为半径的圆与AC切于点D,交BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,△ABC中,∠A=60°,BC为定长,以BC为直径的⊙O分别交AB、AC于点D、E.连接DE、OE.下列结论:①BC=2DE;②D点到OE的距离不变;③BD+CE=2DE;④AE为外接圆的切线.其中正确的结论是( )
已知:如图,△ABC中,∠A=60°,BC为定长,以BC为直径的⊙O分别交AB、AC于点D、E.连接DE、OE.下列结论:①BC=2DE;②D点到OE的距离不变;③BD+CE=2DE;④AE为外接圆的切线.其中正确的结论是( )| A、①② | B、③④ | C、①②③ | D、①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
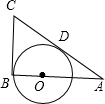 已知:如图,△ABC中,∠B=90°,O是AB上一点,以点O为圆心,OB为半径的圆切AC于点D.
已知:如图,△ABC中,∠B=90°,O是AB上一点,以点O为圆心,OB为半径的圆切AC于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图Rt△ABC中,∠C=Rt∠,AB=5,BC=4.
已知:如图Rt△ABC中,∠C=Rt∠,AB=5,BC=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com