解:(1)由抛物线与X轴的两个交点A、B的坐标,
可以由两根式设抛物线解析式为:y=a(x+2)(x-4),
然后将C点坐标代入得:a(3+2)(3-4)=3,
解得:a=-

,
故抛物线解析式是:y=-

(x+2)(x-4);
(2)由C、B两点坐标利用待定系数法可以求得CB直线方程为:y=-3x+12,
∵CD⊥CB,
∴CD直线方程可以设为:
y=

x+m,
将C点坐标代入得:m=2,
∴CD直线方程为:y=

x+2,
∴D点坐标为:D(0,2),
由抛物线解析式可以顶点公式或对称轴x=1解得顶点M坐标为M(1,
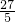
),
∴由C、M两点坐标可以求得CM即CF直线方程为:y=-

x+
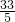
,
∴F点坐标为:F(0,
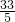
),
∴CE直线方程可以设为:y=

x+n,
将C点坐标代入得:n=

,
∴CE直线方程为:y=

x+

,
令y=0,解得:x=-

,
∴E点坐标为E(-

,0),
∴能;
(3)由C、D两点坐标可以求得CD=

,
则△FDC是等腰△可以有三种情形:
①FD=CD=

,
则F点坐标为F(0,2+

),
②FC=CD=

,过C点作y轴垂线,垂足为H点,
则DH=1,
则FH=1,
则F点坐标为F(0,4),
③FD=FC,作DC的中垂线FG,交y轴于F点,交DC于G点,
由中点公式得G点坐标为G(

,

),
由DC两点可以求得DC直线方程为:y=

x+2,
则FG直线方程可以设为:y=-3x+p,
将G点坐标代入解得:p=7,
故F点坐标为(0,7).
分析:(1)由抛物线与X轴的两个交点A、B的坐标,可以由两根式设抛物线解析式为:y=a(x+2)(x-4),求出a的值即可;
(2)由C、B两点坐标利用待定系数法可以求得CB直线方程为:y=-3x+12,设CD直线方程可以设为:y=

x+m,求出m的值,进而求出D点的值,由抛物线解析式可以顶点公式或对称轴x=1解得顶点M坐标,由C、M两点坐标可以求得CM即CF直线方程,CE直线方程可以设为:y=

x+n,求出n的值,进而求出E点的坐标;
(3)由C、D两点坐标可以求得CD=

,△FDC是等腰△可以有三种情形:①当FD=CD;②FC=CD;③FD=FC,分别求出F点的坐标即可;
点评:本题主要考查二次函数的综合题的知识点,解答本题的关键是熟练掌握二次函数的性质及其解析式的求法,特别是(3)问需要分类讨论,此题难度较大,希望同学们仔细作答.

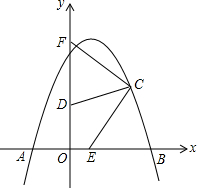
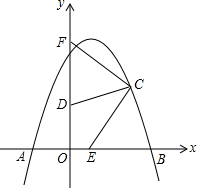 如图,点A(-2,0)、B(4,0)、C(3,3)在抛物线y=ax2+bx+c上,点D在y轴上,且DC⊥BC,∠BCD绕点C顺时针旋转后两边与x轴、y轴分别相交于点E、F.
如图,点A(-2,0)、B(4,0)、C(3,3)在抛物线y=ax2+bx+c上,点D在y轴上,且DC⊥BC,∠BCD绕点C顺时针旋转后两边与x轴、y轴分别相交于点E、F. ,
, (x+2)(x-4);
(x+2)(x-4); x+m,
x+m, x+2,
x+2,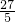 ),
), x+
x+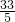 ,
,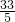 ),
), x+n,
x+n, ,
, x+
x+ ,
, ,
, ,0),
,0), ,
, ,
, ),
),
 ,过C点作y轴垂线,垂足为H点,
,过C点作y轴垂线,垂足为H点, ,
, ),
), x+2,
x+2, x+m,求出m的值,进而求出D点的值,由抛物线解析式可以顶点公式或对称轴x=1解得顶点M坐标,由C、M两点坐标可以求得CM即CF直线方程,CE直线方程可以设为:y=
x+m,求出m的值,进而求出D点的值,由抛物线解析式可以顶点公式或对称轴x=1解得顶点M坐标,由C、M两点坐标可以求得CM即CF直线方程,CE直线方程可以设为:y= x+n,求出n的值,进而求出E点的坐标;
x+n,求出n的值,进而求出E点的坐标; ,△FDC是等腰△可以有三种情形:①当FD=CD;②FC=CD;③FD=FC,分别求出F点的坐标即可;
,△FDC是等腰△可以有三种情形:①当FD=CD;②FC=CD;③FD=FC,分别求出F点的坐标即可;

 阅读快车系列答案
阅读快车系列答案 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°. 如图,点A的坐标为(2
如图,点A的坐标为(2