Question

如图1，过点A（0，4）的圆的圆心坐标为C（2，0），B是第一象限圆弧上的一点，且BC⊥AC，抛物线y=x²+bx+c经过C、B两点，与x轴的另一交点为D．
（1）点B的坐标为（______，______），抛物线的表达式为______；
（2）如图2，求证：BD∥AC；
（3）如图3，点Q为线段BC上一点，且AQ=5，直线AQ交⊙C于点P，求AP的长．

Answer 1

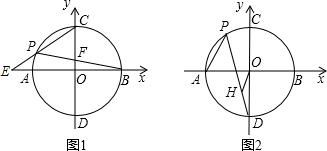
（1）解：如答图1所示，过点B作BE⊥x轴于点E．

∵AC⊥BC，
∴∠ACO+∠BCE=90°，
∵∠ACO+∠OAC=90°，∠BCE+∠CBE=90°，
∴∠OAC=∠BCE，∠ACO=∠CBE．
∵在△AOC与△CEB中，

∴△AOC≌△CEB（ASA）．
∴CE=OA=4，BE=OC=2，
∴OE=OC+CE=6．
∴B点坐标为（6，2）．
∵点C（2，0），B（6，2）在抛物线y=x²+bx+c上，
∴，
解得b=，c=-7．
∴抛物线的表达式为：y=x²+x-7．

（2）证明：在抛物线表达式y=x²+x-7中，令y=0，即x²+x-7=0，
解得x=2或x=7，∴D（7，0）．
如答图2所示，过点B作BE⊥x轴于点E，则DE=OD-OE=1，CD=OD-OC=5．

在Rt△BDE中，由勾股定理得：BD===；
在Rt△BCE中，由勾股定理得：BC===．
在△BCD中，BD=，BC=，CD=5，
∵BD²+BC²=CD²
∴△BCD为直角三角形，∠CBD=90°，
∴∠CBD=∠ACB=90°，
∴AC∥BD．

（3）解：如答图3所示：
由（2）知AC=BC=，又AQ=5，
则在Rt△ACQ中，由勾股定理得：CQ===．

过点C作CF⊥PQ于点F，
∵S_△ACQ=AC•CQ=AQ•CF，
∴CF===2．
在Rt△ACF中，由勾股定理得：AF===4．
由垂径定理可知，AP=2AF，
∴AP=8．
分析：（1）如答图1，作辅助线，证明△AOC≌△CEB，由此得到点B的坐标；再由点C、B的坐标，利用待定系数法求出抛物线的表达式；
（2）如答图2，作辅助线，求出△BCD三边的长度，再利用勾股定理的逆定理判定其为直角三角形，从而问题得证；
（3）如答图3，利用勾股定理依次求出CQ、CF、AF的长度，然后利用垂径定理AP=2AF求出AP的长度．
点评：本题是二次函数综合题型，考查了二次函数的图象与性质、待定系数法、全等三角形、勾股定理、勾股定理的逆定理、垂径定理等知识点．本题设计考点清晰，层次合理：第（1）问主要考查全等三角形和待定系数法，第（2）问主要考查勾股定理及其逆定理，第（3）问主要考查垂径定理与勾股定理．