
 能否表示为3个互异的正整数的倒数的和?
能否表示为3个互异的正整数的倒数的和? 能否表示为3个互异的完全平方数的倒数的和?如果能,请给出一个例子;如果不能,请说明理由.
能否表示为3个互异的完全平方数的倒数的和?如果能,请给出一个例子;如果不能,请说明理由. ,
, .
. 能表示为3个互异的正整数的倒数的和(表示法不唯一).
能表示为3个互异的正整数的倒数的和(表示法不唯一).
 ,
, ,
, ,
, ,并且
,并且 ,
, ,没有一个是完全平方数,
,没有一个是完全平方数, 无解.
无解. .
. 不是整数.
不是整数. 不能表示为3个互异的完全平方数的倒数之和.
不能表示为3个互异的完全平方数的倒数之和. 能否表示为3个互异的完全平方数的倒数之和,各给,共;
能否表示为3个互异的完全平方数的倒数之和,各给,共; 证明即可;
证明即可; 的整数.
的整数.

科目:初中数学 来源: 题型:
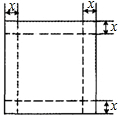 盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
盖的长方体,设长方体的容积为Vcm3,请回答下列问题:| x(cm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| V(cm3) | 324 | 512 | 500 | 384 | 252 |
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
①速度v>0,表示汽车向数轴正方向行驶;速度v<0,表示汽车向数轴负方向行驶;速度v=0,表示汽车静止.
②汽车位置在数轴上的坐标s>0,表示汽车位于零千米路标的右侧;汽车位置在数轴上的坐标s<0,表示汽车位于零千米路标的左侧;汽车位置在数轴上的坐标s=0,表示汽车恰好在零千米路标处.遵照上述约定,将这两辆汽车在公路上匀速行驶的情况,以一次函数图象的形式画在了同一直角坐标系中(如图).
请回答下列问题:
(1)就这两个一次函数图象所反映的两汽车在这条公路上行驶的状况填写如下的表格:

(2)甲、乙两车能否相遇?如能相遇,求相遇时的时刻及在公路上的位置;如不能相遇,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:044
甲、乙两辆汽车在一条公路上匀速行驶,为了确定汽车的位置,我们用数轴Ot表示这条公路,原点O为零千米的路标(如图)并作如下约定:
(1)速度v>0,表示汽车向数轴正方向行驶;速度v<0,表示汽车向数轴负方向行驶;速度v=0,表示汽车静止.
(2)汽车位置在数轴上的坐标s>0,表示汽车位于零千米路标的右侧;汽车位置在数轴上的坐标s=0,表示汽车恰好位于零千米路标处.汽车位置在数轴上的坐标s<0,表示汽车位于零千米路标的左侧.遵照上述约定,将这两辆汽车在公路上匀速行驶的情况,以一次函数图象的形式画在了同一直角坐标系中,如图.
请回答下列问题:
①就这两个一次函数图象所反映的两汽车在这条公路行行驶的状况填写如下表格:

(2)甲、乙两车能否相遇?如能相遇,求相遇时的时刻及在公路上的位置;如不能相遇,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
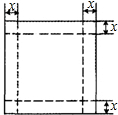 盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
盖的长方体,设长方体的容积为Vcm3,请回答下列问题:| x(cm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| V(cm3) | 324 | 512 | 500 | 384 | 252 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com