练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    补充下列证明过程．

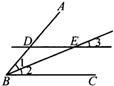
    已知：如图，AB∥CD，∠B＝120°，CA平分∠BCD．

    求证：∠1＝30°．

    证明：因为AB∥CD，(　　)

    所以∠B＋∠BCD＝________．(　　)

    因为∠B＝________，(　　)

    所以∠BCD＝________．

    又因为CA平分∠BCD，(　　)

    所以∠2＝________．(　　)

    因为AB∥CD，(　　)

    所以∠1＝________＝30°．(　　)

    答案：
    解析：

    已知；180°，两直线平行，同旁内角互补；120°，已知；60°；已知；30°，角平分线的定义；已知；∠2，两直线平行，内错角相等


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    22、我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等．那么在什么情况下，它们会全等？
    （1）阅读与证明：
    对于这两个三角形均为直角三角形，显然它们全等．
    对于这两个三角形均为钝角三角形，可证它们全等（证明略）．
    对于这两个三角形均为锐角三角形，它们也全等，可证明如下：
    已知：△ABC、△A1B1C1均为锐角三角形，AB=A1B1，BC=B1Cl，∠C=∠Cl．
    求证：△ABC≌△A1B1C1．
    （请你将下列证明过程补充完整．）
    证明：分别过点B，B1作BD⊥CA于D，
    B1D1⊥C1A1于D1．
    则∠BDC=∠B1D1C1=90°，
    ∵BC=B1C1，∠C=∠C1，
    ∴△BCD≌△B1C1D1，
    ∴BD=B1D1．
    （2）归纳与叙述：
    由（1）可得到一个正确结论，请你写出这个结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    16、请把下列证明过程补充完整：
    已知：如图，DE∥BC，BE平分∠ABC．求证：∠1=∠3．
    证明：因为BE平分∠ABC（已知），
    所以∠1=
    ∠2
    （角平分线性质）．
    又因为DE∥BC（已知），
    所以∠2=
    ∠3
    （两直线平行，同位角相等）．
    所以∠1=∠3（角平分线性质）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    17、将下列证明过程补充完整：
    已知：如图，点B、E分别在AC、DF上，AF分别交BD、CE于点M、N，∠l=∠2，∠A=∠F．
    求证：∠C=∠D．
    证明：因为∠l=∠2    （    已知   ）．
    又因为∠l=∠ANC      （
    对顶角相等
    ），
    所以
    ∠2=∠ANC
     （  等量代换    ）．
    所以
    DB
    ∥
    EC
    （同位角相等，两直线平行）．
    所以∠ABD=∠C        （
    两直线平行，同位角相等
    ）．
    又因为∠A=∠F        （  已知  ），
    所以
    DF
    ∥
    AC
    （
    内错角相等，两直线平行
    ）．
    所以
    ∠D=∠ABD
    （两直线平行，内错角相等）．
    所以∠C=∠D     （
    等量代换
    ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网请把下列证明过程补充完整．
    已知：如图，DE∥BC，BE平分∠ABC．求证：∠1=∠3．
    证明：因为BE平分∠ABC（已知），
    所以∠1=
     
    ．
    又因为DE∥BC（已知），
    所以∠2=
     
    ．
    所以∠1=∠3
     
    ．

    查看答案和解析>>

    同步练习册答案