解:△ABE≌△ACD,∠FAE=∠EAD或△BFD≌△CFE(写出两个即可)
(1)选△ABE≌△ACD.
证明:∵点D,E分别是AB,AC的中点,
∴

.
又∵AB=AC,
∴AD=AE.
在△ABE和△ACD中,
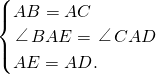
,
∴△ABE≌△ACD(SAS).
(2)选△BCD≌△CBE.
证明:∵AB=AC,∴∠ABC=∠ACB(等边对等角).
∵点D,E分别是AB,AC的中点,
∴
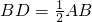
,
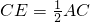
.
∴BD=CE.
在△BCD和△CBE中,
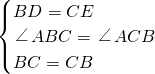
,
∴△BCD≌△CBE(SAS).
(3)选△BFD≌△CFE.
方法一:
证明:∵点D,E分别是AB,AC的中点,
∴

,
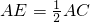
又∵AB=AC,∴AD=AE
在△ABE和△ACD中,

∴△ABE≌△ACD(SAS)
∴∠ABE=∠ACD(全等三角形对应角相等)
∵点D,E分别是AB,AC的中点,∴
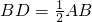
,
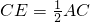
∵AB=AC,∴BD=CE
在△BFD和△CFE中,
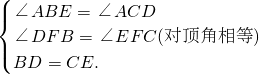
M(m,0)
方法二:
证明:∵AB=AC,
∴∠ABC=∠ACB(等边对等角).
∵点D,E分别是AB,AC的中点,
∴
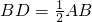
,
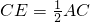
.
∴BD=CE.
在△BCD和△CBE中,
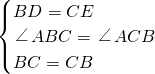
,
∴△BCD≌△CBE(SAS).
∴∠BDC=∠CEB(全等三角形对应角相等).
在△BFD和△CFE中,
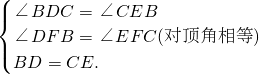
,
∴△BFD≌△CFE(AAS).
分析:根据AB=AC,点D、E分别是AB、AC的中点,得到相等的线段和相等的角,从而可知全等的三角形有:△BCD≌△CBE;△DBF≌△EFC.
点评:本题考查三角形全等的判定及等腰三角形的性质;判定两个三角形全等的一般方法有:SSS、SAS、SSA、AAS、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

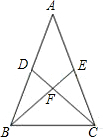 如图,在△ABC中,AB=AC,点D、E分别是AB、AC的中点,点F是BE、CD的交点.请写出图中两组全等的三角形,并选出其中一组加以证明.(要求:写出证明过程中的重要依据)
如图,在△ABC中,AB=AC,点D、E分别是AB、AC的中点,点F是BE、CD的交点.请写出图中两组全等的三角形,并选出其中一组加以证明.(要求:写出证明过程中的重要依据) .
.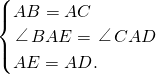 ,
,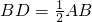 ,
,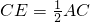 .
.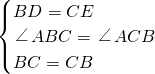 ,
, ,
,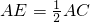

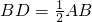 ,
,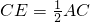
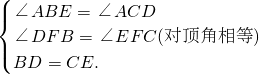 M(m,0)
M(m,0)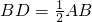 ,
,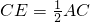 .
.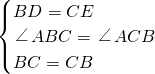 ,
,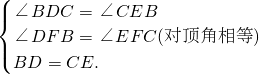 ,
,

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为