Question

如图，△ABC内接于⊙O，高BE、AD交于点P．延长BD、CE，分别交⊙O于点M、N．求证：

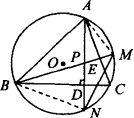
(1)PE＝ME，PD＝ND．

(2)点C为△PMN的外心．

Answer 1

答案：
解析：

解答：(1)连结AM、BN． 　　∵BD、CE是高， 　　∴∠CBE＋∠ACB＝∠CAD＋∠ACB＝90°，∴∠CBE＝∠CAD． 　　∵∠CBE＝∠CAM，∴∠CAD＝∠CAM． 　　∵AE＝AE，∠AEP＝∠AEM＝90°，∴△AEP≌△AEM(SAS)． 　　∴PE＝ME． 　　同法可证　　△BDP≌△BDN，故PD＝ND; 　　(2)由(1)知PE＝ME，AC⊥PM，∴AC垂直平分PM． 　　同理可得BC垂直平分PN． 　　∴点C为△PMN的两边PM、PN的垂直平分线的交点(易得：CM＝CP＝CN)，∴点C为△PMN的外心． 　　评析：这是关于三角形外接圆的又一研究，其中的诸多等线段的证明在近年来的不少中考试题中都曾有所出现．

提示：

欲证PE＝ME，PD＝ND，即需证AC垂直平分PM，BC垂直平分PN．