解:(1)因为抛物线y=ax
2+bx+c经过A(1,0)、B(5,0)两点,
所以二次函数的对称轴为x=
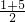
=3,
因为其最低点的纵坐标为-4,
故顶点坐标为(3,-4).
设解析式为
y=a(x-3)
2-4;
将A(1,0)代入解析式得a(1-3)
2-4=0,
即a=1,
解析式为y=(x-3)
2-4,
化为一般式得抛物线的函数解析式为:y=x
2-6x+5;(本小题3分)
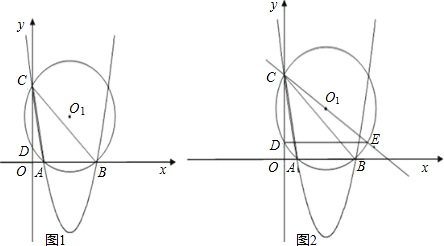
(2)tan∠ACB=

.
过点O
1作O
1P⊥x轴于P,连接O
1A,
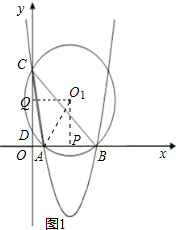
由抛物线与圆的对称性可知O
1P所在的直线是抛物线的对称轴.
故OP=3,AP=OP-OA=2,由CD=AB得:CD=AB=4
过点O
1作O
1Q⊥y轴于Q,由垂径定理得:DQ=CQ=2,O
1P=OQ=OC-CQ=3,
故tan∠ACB=tan∠AO
1P=
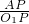
=

;(本小题3分)
(3)①设CE交x轴于F
1,
因为DE∥AB,所以∠DEC=∠OFC,∠COF
1=∠CDE,
所以△OCF
1∽△DCE.
直线CF
1过C(0,5),O(3,3),
得其解析式为y=-

x+5;
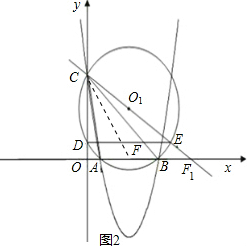
当y=0时,得x=

,所以F
1(

,0).
②△OCF
2与△DCE相似时,根据对称性,由①可以求出x轴上另一点F
2(-

,0).
③△OCF
3与△DEC相似时,
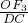
=
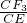
,
即
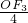
=
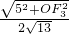
,
两边平方得OF
3=±

.
存在点F,点F的坐标分别为:
F
1(

,0)、F
2(
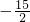
,0)、F
3(

,0)、F
4(
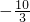
,0).
(适当写出过程,每求出一个点得1分)
分析:(1)根据抛物线y=ax
2+bx+c经过A(1,0)、B(5,0)两点,可得函数对称轴方程,又因为函数最低点的纵坐标为-4,所以可求的抛物线顶点坐标,设出抛物线顶点式,利用待定系数法解答即可;
(2)作出辅助线,过点O
1作O
1P⊥x轴于P,连接O
1A,构造有一角∠AO
1P与∠ACB相等的直角三角形,并求出相应边长,根据正切函数定义解答;
(3)①由(2)中结论,直线CF
1过C(0,5),O(3,3),可求出CF
1的解析式,易得F
1的坐标;
②根据对称性,由①可以求出x轴上另一点F
2(-

,0).
③④△OCF
3与△DEC时,根据相似三角形的性质求出OF
3的横坐标.
点评:此题综合考查了用待定系数法求二次函数的解析式,二次函数的性质和圆周角与圆心角的关系等基础知识,还结合相似三角形的性质考查了点的存在性问题,有一定的难度.

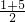 =3,
=3, .
.
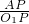 =
= ;(本小题3分)
;(本小题3分) x+5;
x+5;
 ,所以F1(
,所以F1( ,0).
,0). ,0).
,0).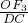 =
=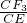 ,
,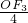 =
=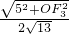 ,
, .
. ,0)、F2(
,0)、F2(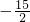 ,0)、F3(
,0)、F3( ,0)、F4(
,0)、F4(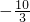 ,0).
,0). ,0).
,0).

 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).