直角三角形两直角边长是3cm和4cm,以该三角形的边所在直线为轴旋转一周所得到的几何体的表面积是________cm2.(结果保留π)
24π,36π,
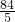
π
分析:先利用勾股定理进行出斜边=5(cm),然后分类讨论:当以3cm的边所在直线为轴旋转一周时;当以4cm的边所在直线为轴旋转一周时;当以5cm的边所在直线为轴旋转一周时,再利用圆锥的侧面展开图为扇形和扇形的面积公式计算即可.
解答:三角形斜边=

=5(cm),
当以3cm的边所在直线为轴旋转一周时,其所得到的几何体的表面积=π•4
2+

•5•2π•4=36π(cm
2);
当以4cm的边所在直线为轴旋转一周时,其所得到的几何体的表面积=π•3
2+

•5•2π•3=24π(cm
2);
当以5cm的边所在直线为轴旋转一周时,其所得到的几何体为共一个底面的两圆锥,其底面圆的半径=

cm,所以此几何体的表面积=

•2π•

•3+

•2π•

•4=
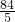
π(cm
2).
故答案为24π,36π,
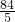
π.
点评:本题考查了圆锥的计算:圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长,扇形的半径等于圆锥的母线长.

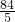 π
π =5(cm),
=5(cm), •5•2π•4=36π(cm2);
•5•2π•4=36π(cm2); •5•2π•3=24π(cm2);
•5•2π•3=24π(cm2); cm,所以此几何体的表面积=
cm,所以此几何体的表面积= •2π•
•2π• •3+
•3+ •2π•
•2π• •4=
•4=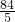 π(cm2).
π(cm2).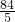 π.
π.

 启东小题作业本系列答案
启东小题作业本系列答案