
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P在AB上,AP=2,点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t/秒(t>0),正方形EFGH与△ABC重叠部分面积为S.
1.当时t=1时,正方形EFGH的边长是 .当t=3时,正方形EFGH的边长是 .
2.当0<t≤2时,求S与t的函数关系式;
3.直接答出:在整个运动过程中,当t为何值时,S最大?最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
如果两个正数 ,即
,即![]() ,有下面的不等式:
,有下面的不等式:
![]() 当且仅当
当且仅当![]() 时取到等号
时取到等号
我们把 叫做正数
叫做正数![]() 的算术平均数,把
的算术平均数,把![]() 叫做正数
叫做正数![]() 的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数。它在数学中有广泛的应用,是解决最值问题的有力工具。下面举一例子:
例:已知 ,求函数
,求函数![]() 的最小值。
的最小值。
解:令 ,则有
,则有![]() ,得
,得![]() ,当且仅当
,当且仅当![]() 时,即
时,即![]() 时,函数有最小值,最小值为
时,函数有最小值,最小值为![]() 。
。
根据上面回答下列问题
1.已知 ,则当
,则当![]() 时,函数
时,函数![]() 取到最小值,最小值
取到最小值,最小值
为
2.用篱笆围一个面积为![]() 的矩形花园,问这个矩形的长、宽各为多少时,所
的矩形花园,问这个矩形的长、宽各为多少时,所
用的篱笆最短,最短的篱笆周长是多少
3.已知![]() ,则自变量
,则自变量![]() 取何值时,函数
取何值时,函数![]() 取到最大值,最大值为多少?
取到最大值,最大值为多少?
查看答案和解析>>
科目:初中数学 来源:2013年江苏省海门市中考二模数学试卷(带解析) 题型:解答题
已知二次函数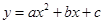 中,其函数
中,其函数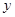 与自变量
与自变量 之间的部分对应值如下表所示:
之间的部分对应值如下表所示:
| x | …… | 0 | 1 | 2 | 3 | 4 | 5 | …… |
| y | …… | 4 | 1 | 0 | 1 | 4 | 9 | …… |
 ,
,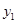 )、B(
)、B(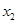 ,
,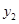 )在该函数的图象上,则当
)在该函数的图象上,则当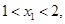
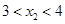 时,
时,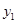 与
与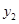 的大小关系是 ;
的大小关系是 ;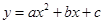 的图象上,问:当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长吗?为什么?=】
的图象上,问:当m<-3时,y1、y2、y3的值一定能作为同一个三角形三边的长吗?为什么?=】查看答案和解析>>
科目:初中数学 来源:2012年北京朝阳区中考模拟数学卷 题型:解答题
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P在AB上,AP=2,点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t/秒(t>0),正方形EFGH与△ABC重叠部分面积为S.
1.当时t=1时,正方形EFGH的边长是 .当t=3时,正方形EFGH的边长是 .
2.当0<t≤2时,求S与t的函数关系式;
3.直接答出:在整个运动过程中,当t为何值时,S最大?最大面积是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com