
 如图,从1×2的矩形ABCD的较短边AD上找一点E,过这点剪下两个正方形,它们的边长分别是AE、DE,当剪下的两个正方形的面积之和最小时,点E应选在
如图,从1×2的矩形ABCD的较短边AD上找一点E,过这点剪下两个正方形,它们的边长分别是AE、DE,当剪下的两个正方形的面积之和最小时,点E应选在 -1):2
-1):2 :1
:1 -1):2
-1):2科目:初中数学 来源: 题型:
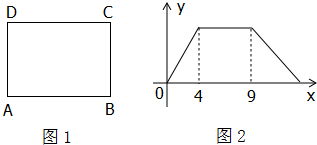 19、如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,若y关于x的函数图象如图2所示,则矩形ABCD的面积是
19、如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,若y关于x的函数图象如图2所示,则矩形ABCD的面积是查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
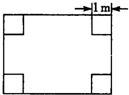 100、张大爷从市场上买回一块矩形铁片,将铁片的四个角各剪出一个边长为1米的正方形,如图所示,剩下的部分刚好能围成一个容积为8米3的无盖长方体且此长方体运输箱底面的长比宽多2米,问张大爷应购买多大的铁皮?
100、张大爷从市场上买回一块矩形铁片,将铁片的四个角各剪出一个边长为1米的正方形,如图所示,剩下的部分刚好能围成一个容积为8米3的无盖长方体且此长方体运输箱底面的长比宽多2米,问张大爷应购买多大的铁皮?查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com