
 x+6分别与x轴、y轴交于点A、B,经过A、B两点的抛物线与x轴的另一交点为C,且其对称轴为x=3.
x+6分别与x轴、y轴交于点A、B,经过A、B两点的抛物线与x轴的另一交点为C,且其对称轴为x=3.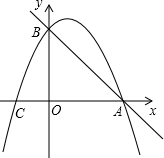 x的函数关系式,这个函数是否有最大值或最小值?如果有,并求这个值和此时点D的坐标;如果没有,说明理由.
x的函数关系式,这个函数是否有最大值或最小值?如果有,并求这个值和此时点D的坐标;如果没有,说明理由.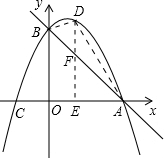 解:(1)直线y=-
解:(1)直线y=- x+6与x、y轴的交点分别为A(8,0)、B(0,6)
x+6与x、y轴的交点分别为A(8,0)、B(0,6)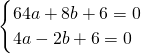

 x2+
x2+ x+6;
x+6;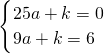
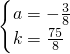
 (x-3)2+
(x-3)2+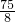
 =10
=10 AB•d=5d
AB•d=5d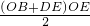 +
+ AE•DE-
AE•DE- OA•OB
OA•OB (x-4)2+4.8
(x-4)2+4.8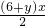 +
+ -
- ×6×8=3x+4y-24
×6×8=3x+4y-24 x2+
x2+ x+6)-24=-
x+6)-24=- x2+12x=-
x2+12x=- (x-4)2+24
(x-4)2+24 (x-4)2+4.8
(x-4)2+4.8 x+6),AB=
x+6),AB= =10
=10 AB•d=5d
AB•d=5d DF•AE+
DF•AE+ DF•OE
DF•OE DF•(AE+OE)=
DF•(AE+OE)= DF•OA=4DF
DF•OA=4DF x+6)]=4(-
x+6)]=4(- x2+
x2+ x+6+
x+6+ x-6)=-
x-6)=- (x-4)2+24
(x-4)2+24 (x-4)2+4.8
(x-4)2+4.8

科目:初中数学 来源: 题型:
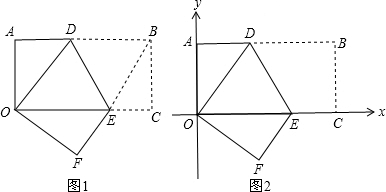 别为x轴、y轴(如图2),求直线EF的函数表达式.
别为x轴、y轴(如图2),求直线EF的函数表达式.查看答案和解析>>
科目:初中数学 来源: 题型:
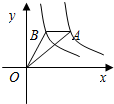 反比例函数y=
反比例函数y=| 6 |
| x |
| 3 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
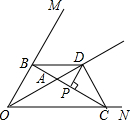 如图所示,点A为∠MON的角平分线上一点,过A任作一直线分别与∠MON的两边交于B、C,P为BC的中点,过P作BC的垂线交OA于点D.∠MON=60°,则∠BDC=( )
如图所示,点A为∠MON的角平分线上一点,过A任作一直线分别与∠MON的两边交于B、C,P为BC的中点,过P作BC的垂线交OA于点D.∠MON=60°,则∠BDC=( )查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)数学来源于生活又服务于生活,利用数学中的几何知识可以帮助我们解决许多实际问题.李明准备与朋友合伙经营一个超市,经调查发现他家附近有两个大的居民区A、B,同时又有相交的两条公路,李明想把超市建在到两居民区的距离、到两公路距离分别相等的位置上,绘制了如图一的居民区和公路的位置图.聪明的你一定能用所学的数学知识帮助李明在图上确定超市的位置!请用尺规作图确定超市P的位置.(写出已知、求作,作图不写作法,但要求保留作图痕迹.)
(1)数学来源于生活又服务于生活,利用数学中的几何知识可以帮助我们解决许多实际问题.李明准备与朋友合伙经营一个超市,经调查发现他家附近有两个大的居民区A、B,同时又有相交的两条公路,李明想把超市建在到两居民区的距离、到两公路距离分别相等的位置上,绘制了如图一的居民区和公路的位置图.聪明的你一定能用所学的数学知识帮助李明在图上确定超市的位置!请用尺规作图确定超市P的位置.(写出已知、求作,作图不写作法,但要求保留作图痕迹.)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com