快捷英语周周练系列答案科目：初中数学 来源：河南省2018届九年级（上）第三次大联考数学试卷 题型：单选题
如图1所示的是带支架功能的某品牌手机壳，将其侧面抽象为如图2所示的几何图形，已知AB=5cm，∠BAC=60°，∠C=45°，则AC的长（
≈1.732，结果精确到0.1cm）为（ ）
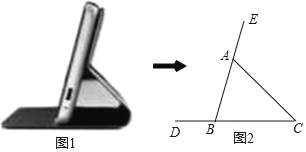
A. 3.4cm B. 4.6cm C. 5.8cm D. 6.8cm
查看答案和解析>>
科目：初中数学 来源：2018年崇明区初三数学二模试卷 题型：填空题
已知袋子中的球除颜色外均相同，其中红球有3个，如果从中随机摸得1个红球的概率为
，那么袋子中共有_________个球．
查看答案和解析>>
科目：初中数学 来源：河南省商丘市柘城县2018届九年级中考数学调研试卷 题型：解答题
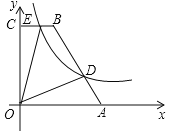
如图，在四边形OABC中，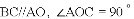
，点
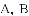
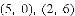
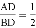，双曲线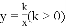
经过点D，交BC于点E
查看答案和解析>>
科目：初中数学 来源：河南省商丘市柘城县2018届九年级中考数学调研试卷 题型：单选题
在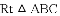
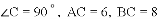，把
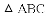
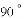得到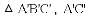
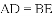
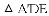
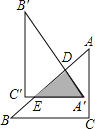
A. 3 B. 5 C. 11 D. 6
查看答案和解析>>
科目：初中数学 来源：2018年内蒙古鄂尔多斯市中考数学对点突破模拟试卷(三) 题型：解答题
【问题情景】利用三角形的面积相等来求解的方法是一种常见的等积法，此方法是我们解决几何问题的途径之一．
例如：张老师给小聪提出这样一个问题：
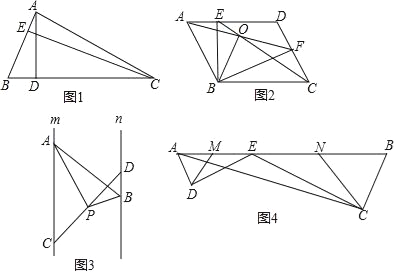
如图1，在△ABC中，AB=3，AD=6，问△ABC的高AD与CE的比是多少？
小聪的计算思路是：
根据题意得：S△ABC=
BC•AD=AB•CE．
从而得2AD=CE，∴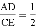
请运用上述材料中所积累的经验和方法解决下列问题：
（1）【类比探究】
如图2，在?ABCD中，点E、F分别在AD，CD上，且AF=CE，并相交于点O，连接BE、BF，
求证：BO平分角AOC．
（2）【探究延伸】
如图3，已知直线m∥n，点A、C是直线m上两点，点B、D是直线n上两点，点P是线段CD中点，且∠APB=90°，两平行线m、n间的距离为4．求证：PA•PB=2AB．
（3）【迁移应用】
如图4，E为AB边上一点，ED⊥AD，CE⊥CB，垂足分别为D，C，∠DAB=∠B，AB=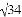
，BC=2，AC=
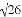，又已知M、N分别为AE、BE的中点，连接DM、CN．求△DEM与△CEN的周长之和．
查看答案和解析>>
科目：初中数学 来源：江苏省无锡市2017-2018学年第二学期七年级数学期中试卷 题型：解答题
某校组织“大手拉小手，义卖献爱心”活动，计划购买黑白两种颜色的文化衫进行手绘设计后出售，并将所获利润全部捐给山区困难孩子．已知该学校从批发市场花3600元购买了黑白两种颜色的文化衫200件．每件文化衫的批发价及手绘后的零售价如下表：
批发价（元） | 零售价（元） | |
黑色文化衫 | 20 | 35 |
白色文化衫 | 15 | 25 |
假设通过手绘设计后全部售出，求该校这次义卖活动所获利润．
查看答案和解析>>
科目：初中数学 来源：四川省绵阳市安州区2018届九年级下学期二诊数学试卷 题型：单选题
如图，平行四边形ABCD中，E是BC边的中点，连接DE并延长交AB的延长线于点F，则在题中条件下，下列结论不能成立的是（ ）
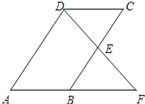
A. BE＝CE B. AB＝BF C. DE＝BE D. AB＝DC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
）÷
，其中m是方程x2+x﹣1=0的根．