练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).

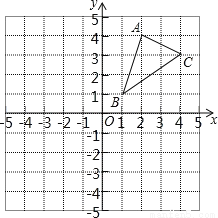
    (1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标；

    (2)请画出△ABC绕点B逆时针旋转90?后的△A2BC2；

    (3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).

    (4)在x轴上有一点P，PA+PB的值最小，请直接写出点P的坐标

    (1)根A1(2,?4),B1(1,?1),C1(4,?3)(2)图形见解析(3) (4)(1.2,0) 【解析】试题分析：（1）利用关于x轴对称点的横坐标相等，纵坐标互为相反数可先找出点A1、B1、C1的坐标，然后画出图形即可； （2）利用旋转的性质可确定出点A2、C2的坐标； （3）先求出BC的长，然后利用弧长公式进行计算即可； （4）连接A1B，与x轴相交于点P，则此...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：解答题

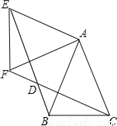
    如图，△ABC中，AB＝AC＝1，∠BAC＝45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE，CF相交于点D。

    （1）求证：BE＝CF ；

    （2）当四边形ACDE为菱形时，求BD的长。

    （1）证明见解析（2）-1 【解析】试题分析：（1）先由旋转的性质得AE=AB，AF=AC，∠EAF=∠BAC，则∠EAF+∠BAF=∠BAC+∠BAF，即∠EAB=∠FAC，利用AB=AC可得AE=AF，于是根据旋转的定义，△AEB可由△AFC绕点A按顺时针方向旋转得到，然后根据旋转的性质得到BE=CD； （2）由菱形的性质得到DE=AE=AC=AB=1，AC∥DE，根据等腰三角形的...

    查看答案和解析>>

    科目：初中数学 来源：广东省东莞市翰林学校2017-2018学年八年级（上）期中数学试卷（word版含答案解析） 题型：解答题

    把下列各数分别填入相应的集合里．

    ﹣5，﹣2.626 626 662…，0，π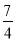，﹣ ，0.12，|﹣6|．

    (1)正数集合：{ …}；

    (2)负数集合：{ …}；

    (3)有理数集合：{ …}；

    (4)无理数集合：{ …}．

    π，0.12，|﹣6|；﹣5，﹣2.626 626 662…，﹣；﹣5，0，﹣，0.12，|﹣6|；﹣2.626 626 662…，π． 【解析】试题分析：依据正数，负数数，有理数，无理数的概念判断即可. 试题解析： 正数集合： 负数集合： 有理数集合： 无理数集合：

    查看答案和解析>>

    科目：初中数学 来源：广东省东莞市翰林学校2017-2018学年八年级（上）期中数学试卷（word版含答案解析） 题型：单选题

    下列实数中，是无理数的为（　　）

    A. 3.14 B. C. D.

    D 【解析】试题分析：无理数就是无限不循环小数．无理数应满足三个条件：①是小数、②是无限小数、③不循环．根据定义可知故选D．

    查看答案和解析>>

    科目：初中数学 来源：广东省东莞市翰林学校2017-2018学年八年级（上）期中数学试卷（word版含答案解析） 题型：单选题

    点A（﹣3，2）关于y轴对称的点的坐标为（　　）

    A. （3，﹣2） B. （3，2） C. （﹣3，﹣2） D. （2，﹣3）

    B 【解析】【解析】 A（﹣3，2）关于y轴对称的点的坐标为（3，2）．故选B．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：填空题

    用等腰直角三角板画∠AOB=45°，将三角板沿OB方向平移到如图所示的虚线M处后绕点M逆时针旋转22°，则三角板的斜边与射线OA的夹角α为_____度．

    22 【解析】试题分析：如图： 由平移的性质知，AO∥SM， 故∠WMS=∠OWM=22°

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型：单选题

    在等腰直角三角形ABC中，AB=AC=4，点O为BC的中点，以O为圆心作半径交BC于点M、N，半圆O与AB、AC相切，切点分别为D、E，则半圆O的半径和的度数分别为（ ）

    A. 2，22.5° B. 3，30° C. 3，22.5° D. 2，30°

    A 【解析】试题分析：∵△ABC为等腰直角三角形， ∴BC＝AB＝，∠B＝45°， ∵点O为BC的中点， ∴OB＝， ∵AB为切线， ∴OD⊥AB， ∴∠ODB＝90°， ∴△ODB为等腰直角三角形， ∴OD＝OB＝×＝2，∠BOD＝45°， ∴∠MND＝∠BOD＝22.5°． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十九章达标检测卷 题型：填空题

    一次函数y=﹣2x+6的图象与x轴交点坐标是______，与y轴交点坐标是______.

    （3，0） （0，6） 【解析】根据一次函数和坐标轴的关系，可知当x=0时，y=6，可知与y轴的交点坐标为（0，6），当y=0时，可知与x轴的交点的坐标为：（3，0）. 故答案为：（3，0），（0，6）.

    查看答案和解析>>

    科目：初中数学 来源：河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    AD，AE分别是△ABC的高和角平分线．

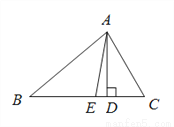
    （1）已知∠B=30°，∠C=60°，求∠DAE的度数；

    （2）设∠B= x，∠C= y（x < y），请直接写出∠DAE的度数 ．（用含x ，y的代数式表示）

    （1）∠EAD=15°;(2) ∠EAD= (y-x) 【解析】分析：分析：（1）根据三角形内角和定理求出∠BAC，再根据角平分线的定义求出∠EAC，根据直角三角形两锐角互余求出∠DAC，然后求解即可．（2）同（1）即可得出结果． 本题解析： （1） 由 ∴ 又AE平分, ∴ ∴ （2）

    查看答案和解析>>

    同步练习册答案