
若点(-5,y1)、(-3,y2)、(3,y3)都在反比例函数y= - 的图像上,则( )
的图像上,则( )
A. y1>y2>y3 B. y2>y1>y3
C. y3>y1>y2 D. y1>y3>y2
B 【解析】∵点(-5,y1)、(-3,y2)、(3,y3)都在反比例函数y=?上, ∴y1=,y2=1,y3=?1. ∵1>>?1, ∴y2>y1>y3, 故选B.科目:初中数学 来源:安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型:填空题
点A(2,-3)关于x轴的对称点A′的坐标是__________;
(2, 3) 【解析】试题分析:两点关于x轴对称,则两点的横坐标相等,纵坐标互为相反数.查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:解答题
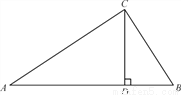
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=20,BC=15.求AB和CD的长.
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:单选题
计算(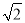 -1)(
-1)(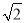 +1)2的结果是( )
+1)2的结果是( )
A. 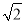 +1 B. 3(
+1 B. 3(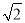 -1) C. 1 D. -1
-1) C. 1 D. -1
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于( )
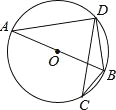
A.16° B.32° C.58° D.64°
B 【解析】 试题分析:根据圆周角定理得到∠ADB=90°,求出∠A的度数,根据圆周角定理解答即可. ∵AB是⊙O的直径, ∴∠ADB=90°, ∴∠A=90°﹣∠ABD=32°, 则∠BCD=∠A=32°查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
下列立体图形中,主视图是三角形的是( )
A.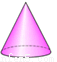 B.
B. C.
C.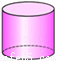 D.
D.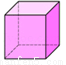
查看答案和解析>>
科目:初中数学 来源:青海省2017-2018学年七年级上学期12月月考数学试卷 题型:解答题
解方程: 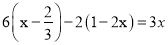
查看答案和解析>>
科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
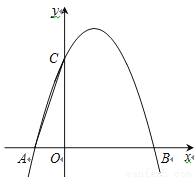
如图,抛物线y=-x 2+bx+c与x轴交于A、B两点,与y轴交于点C,已知经过B、C两点的直线的表达式为y=-x+3.
(1)求抛物线的函数表达式;
(2)点P(m,0)是线段OB上的一个动点,过点P作y轴的平行线,交直线BC于D,交抛物线于E,EF∥x轴,交直线BC于F,DG∥x轴,FG∥y轴,DG与FG交于点G.设四边形DEFG的面积为S,当m为何值时S最大,最大值是多少?
(3)在坐标平面内是否存在点Q,将△OAC绕点Q逆时针旋转90°,使得旋转后的三角形恰好有两个顶点落在抛物线上.若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.
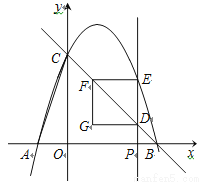
查看答案和解析>>
科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:填空题
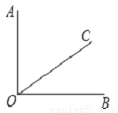
如图,∠AOB=90°,∠AOC=2∠BOC,则∠BOC=________°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com