
分析 先对所求式子进行化简,然后根据a=2,b=$\frac{1}{3}$可以求得化简后式子的值,本题得以解决.
解答 解:$\frac{a}{a-b}$($\frac{1}{b}$-$\frac{1}{a}$)+$\frac{a-1}{b}$
=$\frac{a}{a-b}•\frac{a-b}{ab}+\frac{a-1}{b}$
=$\frac{1}{b}+\frac{a-1}{b}$
=$\frac{a}{b}$,
当a=2,b=$\frac{1}{3}$时,原式=$\frac{2}{\frac{1}{3}}=6$.
点评 本题考查分式的化简求值,解题的关键是会对所求的式子化简并求值.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:填空题
 如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧$\widehat{BC}$的长为$\frac{4π}{3}$.
如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧$\widehat{BC}$的长为$\frac{4π}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
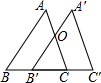 如图,△ABC中,BC=5cm,将△ABC沿BC方向平移至△A′B′C′的对应位置时,A′B′恰好经过AC的中点O,则△ABC平移的距离为2.5cm.
如图,△ABC中,BC=5cm,将△ABC沿BC方向平移至△A′B′C′的对应位置时,A′B′恰好经过AC的中点O,则△ABC平移的距离为2.5cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com