
�ð���Ƥ����ͷ�У�ÿ����Ƥ���ƺ���15������е�40����һ�������������е����һ��ͷ�У�����280�Ű���Ƥ���ö������ƺ������������ƺеף����������Ƴ�����ͷ�У����з��̼��㣩
��160���ƺ�����120���ƺеף� ������������������������⣬�ҵ�������ϵ��һ�������������е����һ�ף����е�����=������������2���з�����⼴��. ����������������� ����x���ƺ��������ã�280��x�����ƺеף�������ã� 2��15x=40��280��x���� ��ã�x=160�� 280��x=120�� ����160���ƺ�����120���ƺеף� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㽭�����ϳ���������ѧ2017-2018ѧ����꼶��ѧ���п�����ѧ�Ծ� ���ͣ������
�����в���ʽ�Ͳ���ʽ�飮
��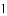
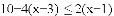
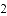
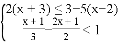 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꽭��ʡ�������п���ѧģ���Ծ� ���ͣ���ѡ��
����ͳ�ƾֵ���������ʾ������Ŀǰ��ס�˿�ԼΪ4470000�ˣ����ݡ�4470000���ÿ�ѧ�������ɱ�ʾΪ��������
A. 4.47��106 B. 4.47��107 C. 0.447��107 D. 447��104
A ����������ѧ�������ı�ʾ��ʽΪa��10n����ʽ������1��|a|��10��nΪ������ȷ��n��ֵʱ����ԭ��������λ����1������ 4470000= 4.47��106����ѡA.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡͭ����������2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
9������ƽ������____________��
3 ��������9������ƽ������3. �ʴ�Ϊ3.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡͭ����������2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ���ѡ��
������3.0��10 ��ȷ���� )
��ȷ���� )
A. ʮ��λ B. ��λ C. ʮλ D. ��λ
C ��������3.0��102=300����ȷ��ʮλ. ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ���ص���Э����2017-2018ѧ�����ѧ�ڵڶ����¿����꼶��ѧ�Ծ� ���ͣ������
���㣺��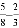 ����24��
����24�� �£�
�£�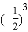 ��|��22|.
��|��22|.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ���ص���Э����2017-2018ѧ�����ѧ�ڵڶ����¿����꼶��ѧ�Ծ� ���ͣ���ѡ��
���и������У��٩�22��22 ��-����33����33 ��|��2|�멁|��2| �ܣ���33���멁33 �ݩ���+3����+����3��������ȵĹ��У�������
A. 4�� B. 3�� C. 2�� D. 1��
B ���������������������ص��Լ������Ľ������֪-22��22����ȣ���-��-33��=33��������ȣ��ɾ���ֵ�����ʣ���֪|-2|=2��-|-2|=-2������ȣ���-33��=-33��������ȣ���-��+3��=-3��+��-3��=-3��������ȣ�����ȵĹ���3��. ��ѡ��B.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ��� ���꼶��ѧ��ĩ���Ծ� ���ͣ������
�Ȼ�������ֵ: 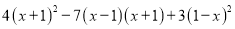 ������
������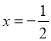
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������б������ڶ���2017-2018ѧ����꼶12���¿���ѧ�Ծ� ���ͣ������
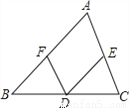
��ͼ���ڡ�ABC�У�DΪBC�ߵ��е㣬��D��ֱ���DE��AB��AC�ڵ�E��DF��AC��AB�ڵ�F��
��֤��BF=DE��
���𰸡�֤��������
�������������������������Ա߷ֱ�ƽ�е��ı���Ϊƽ���ı��ο��ж��ı���AFDE��ƽ���ı��Σ�����ƽ���ı��ε����ʿɵ�DE=AF������DΪBC�ߵ��е㣬DF��AC���ɵ�BF=AF�����ɵ�BF=DE��
���������
��DE��AB��DF��AC��
��DE��AF��DF��AE��
���ı���AFDE��ƽ���ı��Σ�
��DE=AF��
��DΪBC�ߵ��е㣬
��BD=DC����DF��AC��
��BF=AF��
��BF=DE��
�����͡������
��������
26
��ͼ����֪����C=��D��OD=OC����֤��DE=CE��
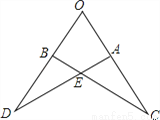
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com