
 如图所示:B、C、D三点在一条直线上,△ABC和△ECD是等边三角形.求证:BE=AD.
如图所示:B、C、D三点在一条直线上,△ABC和△ECD是等边三角形.求证:BE=AD.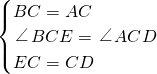


科目:初中数学 来源: 题型:
 24、如图所示,向平静的水面投入一枚石子,在水面会激起一圈圈圆形涟漪,当半径从2cm变成5cm时,圆形的面积从
24、如图所示,向平静的水面投入一枚石子,在水面会激起一圈圈圆形涟漪,当半径从2cm变成5cm时,圆形的面积从查看答案和解析>>
科目:初中数学 来源: 题型:
 4、已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )
4、已知O为圆锥的顶点,M为圆锥底面上一点,点P在OM上.一只蜗牛从P点出发,绕圆锥侧面爬行,回到P点时所爬过的最短路线的痕迹如图所示.若沿OM将圆锥侧面剪开并展开,所得侧面展开图是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com