
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017年湖南省郴州市中考数学模拟试卷 题型:单选题
如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则图中阴影面积(△PEF和△PGH的面积和)等于( )
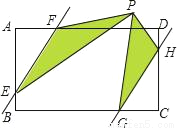
A. 7 B. 8 C. 12 D. 14
A 【解析】连接EG,FH, ∵在矩形ABCD中,AD=6,AB=4,AF=CG=2,BE=DH=1, ∴AE=AB?BE=4?1=3, CH=CD?DH=4?1=3, ∴AE=CH, 在△AEF与△CGH中, , ∴△AEF≌△CGH(SAS), ∴EF=GH, 同理可得,△BGE≌△DFH, ∴EG=FH, ∴四边形EGH...查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:填空题
如图,点F、C在线段BE上,且∠1=∠2,BC=EF,若要使△ABC≌△DEF,则还需补充一个条件________,依据是________.
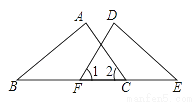
查看答案和解析>>
科目:初中数学 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:解答题
如图,在四边形ABCD中,∠BAD=∠B=∠C=90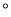 ,AD=BC=20,AB=DC=16.将四边形ABCD沿直线AE折叠,使点D落在BC边上的点F处.
,AD=BC=20,AB=DC=16.将四边形ABCD沿直线AE折叠,使点D落在BC边上的点F处.
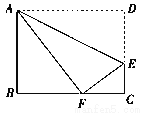
(1)求BF的长;
(2)求CE的长.
(1);(2) 【解析】试题分析:由折叠的性质可得:AF=AD=20,再由勾股定理可求出BF=12. (2)设CE=x,DE=EF=16-x,然后利用勾股定理得到,再解方程求出x即可. (1)∵△AFE是△ADE折叠得到的, ∴. 在Rt△ABE中, (2)∵△AFE是△ADE折叠得到的, ∴. 设,则 在Rt△EFC中, 即 解得...查看答案和解析>>
科目:初中数学 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:解答题
解方程: 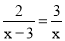
查看答案和解析>>
科目:初中数学 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:单选题
如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )
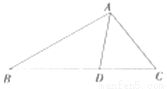
A. 3:2 B. 4:6 C. 9:4 D. 不能确定
A 【解析】试题解析:过点D作DE⊥AB于E,DF⊥AC于F. ∵AD为∠BAC的平分线, ∴DE=DF,又AB:AC=3:2, ∴S△ABD:S△ACD=(AB•DE):(AC•DF)=AB:AC=3:2. 故选A.查看答案和解析>>
科目:初中数学 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:解答题
某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为:w=﹣2x+240.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x的关系式;
(2)当x取何值时,y的值最大?
(3)如果物价部门规定这种绿茶的销售单价不得高于90元/千克,公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元?
(1)y=﹣2x2+340x﹣12000;(2)85;(3)当销售单价为75元时,可获得销售利润2250元. 【解析】试题分析:(1)因为y=(x﹣50)w,w=﹣2x+240 故y与x的关系式为y=﹣2x2+340x﹣12000. (2)用配方法化简函数式求出y的最大值即可. (3)令y=2250时,求出x的解即可. 【解析】 (1)y=(x﹣50)•w=(x﹣5...查看答案和解析>>
科目:初中数学 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:单选题
如图,在Rt△ABC中,∠ACB=90,CD⊥AB,垂足为D,若AC=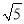 ,BC=2.则sin∠ACD的值为( )
,BC=2.则sin∠ACD的值为( )
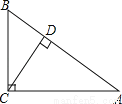
A. 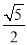 B.
B. 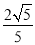 C.
C. 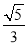 D.
D. 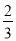
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型:填空题
如图,将函数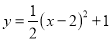 的图象沿
的图象沿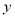 轴向上平移得到一条新函数的图象,其中点
轴向上平移得到一条新函数的图象,其中点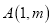 ,
, 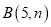 平移后的对应点分别为点
平移后的对应点分别为点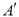 、
、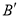 .若曲线段
.若曲线段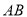 扫过的面积为
扫过的面积为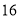 (图中的阴影部分),则新图象的函数表达式是__________.
(图中的阴影部分),则新图象的函数表达式是__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com