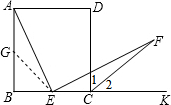
解:(1)取AB的中点G,
∵正方形ABCD,E是BC中点,
∴AG=BG=BE=EC,
∴△BEG是等腰直角三角形,
∴∠BGE=45°,
∠AGE=180°-45°=135°,
∵∠1=∠2,
∴∠ECF=90°+45°=135°,
∴∠AGE=∠ECF,
∵∠AEF=90°,
∴∠AEB+∠CEF=180°-90°=90°,
又∵∠BAE+∠AEB=180°-90°=90°,
∴∠BAE=∠CEF,
在△AGE和△ECF中,
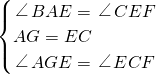
,
∴△AGE≌△ECF(ASA),
∴AE=EF;
(2)结论AE=EF仍然成立.
理由如下:在AB上截取BG=BE,
则△BGE是等腰直角三角形,
∴∠BGE=45°,
∠AGE=180°-45°=135°,
∵AG+BG=AB,BE+EC=BC,AB=BC,
∴AG=EC,
∵∠1=∠2,
∴∠ECF=90°+45°=135°,
∴∠AGE=∠ECF,
∵∠AEF=90°,
∴∠AEB+∠CEF=180°-90°=90°,
又∵∠BAE+∠AEB=180°-90°=90°,
∴∠BAE=∠CEF,
在△AGE和△ECF中,
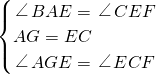
,
∴△AGE≌△ECF(ASA),
∴AE=EF.
分析:(1)取AB的中点G,根据正方形的性质求出AG=BG=BE=EC,然后求出△BEG是等腰直角三角形,再求出∠AGE=135°,∠ECF=135°,从而得到∠AGE=∠ECF,再根据同角的余角相等求出∠BAE=∠CEF,然后利用“角边角”证明△AGE和△ECF全等,根据全等三角形对应边相等求解即可;
(2)在AB上截取BG=BE,得到△BGE是等腰直角三角形,然后求出∠AGE=135°,再根据正方形的性质求出AG=EC,再求出∠ECF=135°,从而得到∠AGE=∠ECF,再根据同角的余角相等求出∠BAE=∠CEF,然后利用“角边角”证明△AGE和△ECF全等,根据全等三角形对应边相等求解即可.
点评:本题考查了正方形的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质,作辅助线并求出∠AGE=∠ECF和AG=EC是解题的关键,也是本题的难点.

 正方形ABCD,E是BC中点,∠AEF=90°,∠1=∠2
正方形ABCD,E是BC中点,∠AEF=90°,∠1=∠2
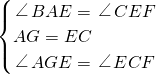 ,
, ,
,

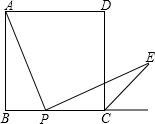 (2013•桂林)如图,已知边长为4的正方形ABCD,P是BC边上一动点(与B、C不重合),连结AP,作PE⊥AP交∠BCD的外角平分线于E.设BP=x,△PCE面积为y,则y与x的函数关系式是( )
(2013•桂林)如图,已知边长为4的正方形ABCD,P是BC边上一动点(与B、C不重合),连结AP,作PE⊥AP交∠BCD的外角平分线于E.设BP=x,△PCE面积为y,则y与x的函数关系式是( )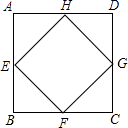 如图,已知正方形ABCD的面积是64cm2,依次连接正方形的四边中点E、F、G、H得到小正方形EFGH.求这个小正方形EFGH的边长(结果保留两个有效数字).
如图,已知正方形ABCD的面积是64cm2,依次连接正方形的四边中点E、F、G、H得到小正方形EFGH.求这个小正方形EFGH的边长(结果保留两个有效数字).