
 在第一象限内的分支上两点,直线CD分别交x轴、y轴于A、B,CG⊥x轴于G,DH⊥x轴于H,
在第一象限内的分支上两点,直线CD分别交x轴、y轴于A、B,CG⊥x轴于G,DH⊥x轴于H, =
=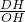 =
= ,OC=
,OC= .
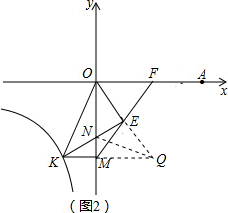
. 在第三象限内的分支上的一动点,过点K作KM⊥y轴于M,OE平分∠KOA,KE⊥OE,KE交y轴于N,直线ME交x轴于F,①
在第三象限内的分支上的一动点,过点K作KM⊥y轴于M,OE平分∠KOA,KE⊥OE,KE交y轴于N,直线ME交x轴于F,① ,②
,② ,有一个为定值,请你选择正确结论并求出这个定值.
,有一个为定值,请你选择正确结论并求出这个定值.
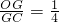 (已知),
(已知), ,
,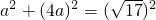
 得:m=1×4=4,即m=4;
得:m=1×4=4,即m=4;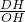 =
= (已知)
(已知) 得:4b2=4b=1
得:4b2=4b=1 (勾股定理).
(勾股定理).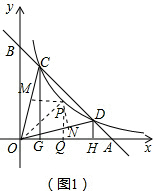
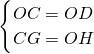 ,
,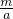 =
= ,
,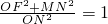 ;
;
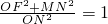 .
.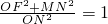 ;如图2,如图2,延长OE、KM交于Q,连接NQ.根据角平分线的性质、平行线的性质以及等腰三角形的判定与性质推知KQ=KO、OE=EQ,即KE是OQ中垂线,所以
;如图2,如图2,延长OE、KM交于Q,连接NQ.根据角平分线的性质、平行线的性质以及等腰三角形的判定与性质推知KQ=KO、OE=EQ,即KE是OQ中垂线,所以

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:




查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| m |
| x |
| OG |
| GC |
| DH |
| OH |
| 1 |
| 4 |
| 17 |
| m |
| x |
| OF2+MN2 |
| ON2 |
| OF+MN |
| ON |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com