
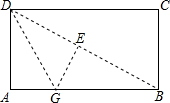
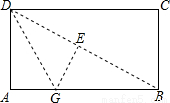
 如图,折叠矩形的纸片ABCD,先折痕(对角线)DB,再过点D折叠,使AD落在折痕BD上,得另一折痕DG,若AB=2,BC=1,则AG=________.
如图,折叠矩形的纸片ABCD,先折痕(对角线)DB,再过点D折叠,使AD落在折痕BD上,得另一折痕DG,若AB=2,BC=1,则AG=________.科目:初中数学 来源: 题型:
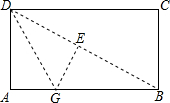 如图,折叠矩形的纸片ABCD,先折痕(对角线)DB,再过点D折叠,使AD落在折痕BD上,得另一折痕DG,若AB=2,BC=1,则AG=
如图,折叠矩形的纸片ABCD,先折痕(对角线)DB,再过点D折叠,使AD落在折痕BD上,得另一折痕DG,若AB=2,BC=1,则AG=
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
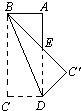 19、如图,将矩形ABCD纸片沿对角线BD折叠,使点C落在C′处,BC'交AD于E,若∠DBC=22.5°,则在不添加任何辅助线的情况下,则图中的等腰三角形有
19、如图,将矩形ABCD纸片沿对角线BD折叠,使点C落在C′处,BC'交AD于E,若∠DBC=22.5°,则在不添加任何辅助线的情况下,则图中的等腰三角形有查看答案和解析>>
科目:初中数学 来源:2011年湖北省黄冈市中考数学模拟试卷(八)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com