
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -6.5 | -4 | -2.5 | -2 | -2.5 | … |
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | |
| 售价x(元/千克) | 18 | 15 | 12 | 10 | 9 |
| 销售量y(千克) | 50 | 60 | 75 | 90 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
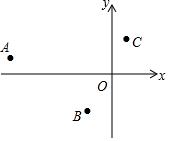 在平面直角坐标系xOy中,二次函数y=ax2+bx的图象经过点A,B,C,则对系数a和b判断正确的是( )
在平面直角坐标系xOy中,二次函数y=ax2+bx的图象经过点A,B,C,则对系数a和b判断正确的是( )| A. | a>0,b>0 | B. | a<0,b<0 | C. | a>0,b<0 | D. | a<0,b>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图已知直线CB∥OA,∠C=∠OAB=100°,点E、点F在线段BC上,满足∠FOB=∠AOB=α,OE平分∠COF.
如图已知直线CB∥OA,∠C=∠OAB=100°,点E、点F在线段BC上,满足∠FOB=∠AOB=α,OE平分∠COF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com