解:(1)∵令y=0,则x=3,令x=0,则y=4,
∴A(3,0),B(0,4),
其函数图象如图1所示:
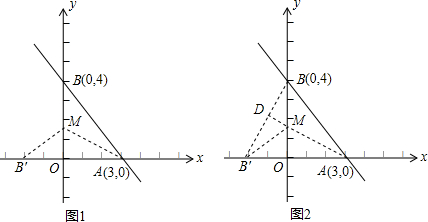
(2)∵A(3,0),B(0,4),
∴OA=3,OB=4,
∴AB=

=

=5,
∵△AMB′由△AMB翻折而成,
∴AB′=AB=5,
∵OA=3,
∴OB′=2,
∴B′(-2,0);
(3)如图2,连接BB′,延长AM交BB′于点D,则点D即为BB′的中点,
∵B(0,4),B′(-2,0),
∴D(-1,2),
设直线AD的解析式为y=kx+b(k≠0),
∵A(3,0),D(-1,2),
∴

,解得

,
∴直线AD的解析式为y=-

x+

,
∵令x=0,则y=

,
∴M(0,

),
∴S
△AMB′=

AB′×OM=

×5×

=

.
分析:(1)先令y=0求出x的值,再令x=0求出y的值即可得到A、B两点的坐标,画出函数图象,再根据翻折变换的性质得出B′、M的大致位置;
(2)先根据勾股定理求出AB的长,再根据图形翻折变换的性质即可得出AB′的长,进而得出B′的坐标;
(3)连接BB′,延长AM交BB′于点D,则点D即为BB′的中点,求出D点坐标,利用待定系数发球出直线AD的解析式,求出直线AD与y轴的交点坐标即为点M的坐标.
点评:本题考查的是一次函数综合题,涉及到用待定系数法求一次函数的解析式及图形翻折变换的性质,根据题意画出图形,利用数形结合求解是解答此题的关键.

 x+4与x轴交于点A、与y轴交于点B,M是线段OB上的一点(O是原点),若△ABM沿AM折叠(AM为折痕),点B恰好落在x轴上的点B′处
x+4与x轴交于点A、与y轴交于点B,M是线段OB上的一点(O是原点),若△ABM沿AM折叠(AM为折痕),点B恰好落在x轴上的点B′处 x+4图象、标出点A、B的准确位置,及B′、M的大致位置;
x+4图象、标出点A、B的准确位置,及B′、M的大致位置;
 =
= =5,
=5, ,解得
,解得 ,
, x+
x+ ,
, ,
, ),
), AB′×OM=
AB′×OM= ×5×
×5× =
= .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案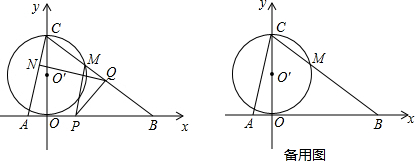
 (2012•兰州)如图,M为双曲线y=
(2012•兰州)如图,M为双曲线y=