在Rt△ABC中,∠C=90°,AB=5,AC=4,△ABC绕点A旋转后点C落在AB边上,点B落在点B′,那么BB′的长为________.

分析:如图,根据题意,△ABC绕点A旋转后得到△AB′C′,可得,AC′=4,AB′=5,B′C′=3,BC′=1,所以,在Rt△B′C′B中,应用勾股定理,即可求得.
解答:
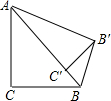
解:如图,∵△ABC绕点A旋转后得到△AB′C′,
∴△ABC≌△AB′C′,
∵∠C=90°,AB=5,AC=4,
∴∠AC′B′=∠B′C′B=90°,AC′=4,AB′=5,
∴B′C′=3,BC′=1,
∴在Rt△B′C′B中,
BB′=
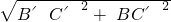
=

=

.
故答案为:

.
点评:本题主要考查了勾股定理和旋转的性质,知道旋转前后的两个图形完全相等,是解答本题的基础;并能熟练应用勾股定理求值.
