解:(1)∵CE∥AB,ED=BC(但ED不平行于BC),
∴四边形BCDE是等腰梯形,
∴∠BDE=∠B,
在Rt△ABC中,∠A=90°-∠B=90°-60°=30°,
∴α=∠BDE-∠A=60°-30°=30°,
∵CE∥AB,
∴∠A=∠OCE,
∵点O是AC的中点,
∴AO=CO,
在△AOD和△COE中,
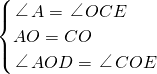
,
∴△AOD≌△COE(ASA),
∴OD=OE,
∵α=∠A=30°,
∴AD=OD,
∴AD=

DE=

BC=

×4=2;
(2)∵ED⊥AB,
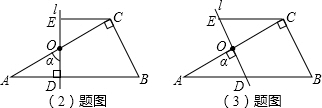
∴α=90°-∠A=90°-30°=60°,
在△ABC中,∵∠B=60°,BC=4,
∴AC=BC•tan60°=4×

=4

,
∵点O是AC的中点,
∴AO=

AC=

×4

=2

,
∴AD=AC•cos30°=2

×

=3;
(3)存在点D为AB的中点时,四边形EDBC为菱形.
此时,BD=

AB,
∵∠ACB=90°,∠A=30°,
∴BC=

AB,
∴BD=BC,
∵点O是AC的中点,点D是AB的中点,
∴DE∥BC,
又∵CE∥AB,
∴四边形EDBC是平行四边形,
∴平行四边形EDBC是菱形,
∴α=∠AOD=∠ABC=90°,
即旋转角α=90°.
分析:(1)先判定四边形BCDE是等腰梯形,再根据等腰梯形同一底上的两底角相等求出∠BDE=∠B,根据直角三角形两锐角互余求出∠A=30°,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解,再证明△AOD和△COE全等,根据全等三角形对应边相等可得OD=OE,然后求解即可;
(2)在Rt△AOD中,利用直角三角形两锐角互余列式求解即可得到α值,解直角三角形求出AC的长,再根据中点的定义求出AO,然后利用∠A的余弦值求解即可得到AD的长;
(3)存在点D为AB的中点时,四边形EDBC为菱形.再根据直角三角形30°角所对的直角边等于斜边的一半BC=BD=

AB,然后根据菱形的判定方法即可判定再根据两直线平行,同位角相等可得α=∠ACB.
点评:本题考查了旋转的性质,解直角三角形,菱形的判定与性质,直角三角形30°角所对的直角边等于斜边的一半的性质,三角形的中位线定理,综合性较强,但难度不大.

 在Rt△ABC中,∠ACB=90°,∠B=60°,BC=4,点O是AC的中点,过点O的直线l从与AC重合的位置开始,绕点O作逆时针旋转,交AB边于点D,过点C作CE∥AB交直线l于E,设直线l的旋转角为α.
在Rt△ABC中,∠ACB=90°,∠B=60°,BC=4,点O是AC的中点,过点O的直线l从与AC重合的位置开始,绕点O作逆时针旋转,交AB边于点D,过点C作CE∥AB交直线l于E,设直线l的旋转角为α.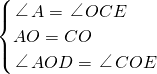 ,
, DE=
DE= BC=
BC= ×4=2;
×4=2;
 =4
=4 ,
, AC=
AC= ×4
×4 =2
=2 ,
, ×
× =3;
=3; AB,
AB, AB,
AB, AB,然后根据菱形的判定方法即可判定再根据两直线平行,同位角相等可得α=∠ACB.
AB,然后根据菱形的判定方法即可判定再根据两直线平行,同位角相等可得α=∠ACB.
